跳转至

73. 矩阵置零

题目描述

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

 

示例 1：

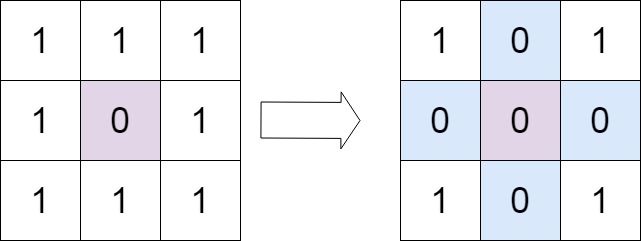
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

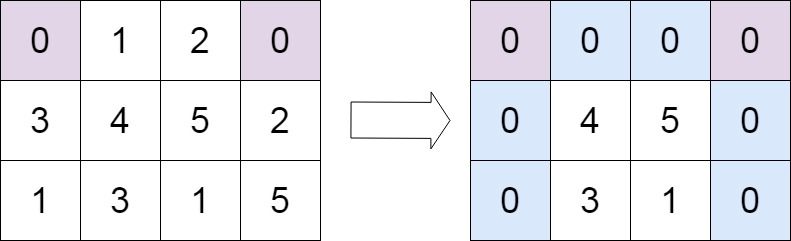
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

 

提示：

  • m == matrix.length
  • n == matrix[0].length
  • 1 <= m, n <= 200
  • -231 <= matrix[i][j] <= 231 - 1

 

进阶：

  • 一个直观的解决方案是使用  O(mn) 的额外空间，但这并不是一个好的解决方案。
  • 一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
  • 你能想出一个仅使用常量空间的解决方案吗？

解法

方法一：数组标记

我们分别用数组 rows 和 cols 标记待清零的行和列。

然后再遍历一遍矩阵，将 rows 和 cols 中标记的行和列对应的元素清零。

时间复杂度 $O(m\times n)$，空间复杂度 $O(m+n)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        m, n = len(matrix), len(matrix[0])
        rows = [0] * m
        cols = [0] * n
        for i, row in enumerate(matrix):
            for j, v in enumerate(row):
                if v == 0:
                    rows[i] = cols[j] = 1
        for i in range(m):
            for j in range(n):
                if rows[i] or cols[j]:
                    matrix[i][j] = 0

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        boolean[] rows = new boolean[m];
        boolean[] cols = new boolean[n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    rows[i] = true;
                    cols[j] = true;
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (rows[i] || cols[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        vector<bool> rows(m);
        vector<bool> cols(n);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (!matrix[i][j]) {
                    rows[i] = 1;
                    cols[j] = 1;
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (rows[i] || cols[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
func setZeroes(matrix [][]int) {
    m, n := len(matrix), len(matrix[0])
    rows := make([]bool, m)
    cols := make([]bool, n)
    for i, row := range matrix {
        for j, v := range row {
            if v == 0 {
                rows[i] = true
                cols[j] = true
            }
        }
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if rows[i] || cols[j] {
                matrix[i][j] = 0
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 Do not return anything, modify matrix in-place instead.
 */
function setZeroes(matrix: number[][]): void {
    const m = matrix.length;
    const n = matrix[0].length;
    const rows: boolean[] = new Array(m).fill(false);
    const cols: boolean[] = new Array(n).fill(false);
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (matrix[i][j] === 0) {
                rows[i] = true;
                cols[j] = true;
            }
        }
    }
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (rows[i] || cols[j]) {
                matrix[i][j] = 0;
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
var setZeroes = function (matrix) {
    const m = matrix.length;
    const n = matrix[0].length;
    const rows = new Array(m).fill(false);
    const cols = new Array(n).fill(false);
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (matrix[i][j] == 0) {
                rows[i] = true;
                cols[j] = true;
            }
        }
    }
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (rows[i] || cols[j]) {
                matrix[i][j] = 0;
            }
        }
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
public class Solution {
    public void SetZeroes(int[][] matrix) {
        int m = matrix.Length, n = matrix[0].Length;
        bool[] rows = new bool[m], cols = new bool[n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    rows[i] = true;
                    cols[j] = true;
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (rows[i] || cols[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

方法二：原地标记

方法一中使用了额外的数组标记待清零的行和列，实际上我们也可以直接用矩阵的第一行和第一列来标记，不需要开辟额外的数组空间。

由于第一行、第一列用来做标记，它们的值可能会因为标记而发生改变，因此，我们需要额外的变量 $i0$, $j0$ 来标记第一行、第一列是否需要被清零。

时间复杂度 $O(m\times n)$，空间复杂度 $O(1)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        m, n = len(matrix), len(matrix[0])
        i0 = any(v == 0 for v in matrix[0])
        j0 = any(matrix[i][0] == 0 for i in range(m))
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][j] == 0:
                    matrix[i][0] = matrix[0][j] = 0
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j] = 0
        if i0:
            for j in range(n):
                matrix[0][j] = 0
        if j0:
            for i in range(m):
                matrix[i][0] = 0

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        boolean i0 = false, j0 = false;
        for (int j = 0; j < n; ++j) {
            if (matrix[0][j] == 0) {
                i0 = true;
                break;
            }
        }
        for (int i = 0; i < m; ++i) {
            if (matrix[i][0] == 0) {
                j0 = true;
                break;
            }
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (i0) {
            for (int j = 0; j < n; ++j) {
                matrix[0][j] = 0;
            }
        }
        if (j0) {
            for (int i = 0; i < m; ++i) {
                matrix[i][0] = 0;
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        bool i0 = false, j0 = false;
        for (int j = 0; j < n; ++j) {
            if (matrix[0][j] == 0) {
                i0 = true;
                break;
            }
        }
        for (int i = 0; i < m; ++i) {
            if (matrix[i][0] == 0) {
                j0 = true;
                break;
            }
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (i0) {
            for (int j = 0; j < n; ++j) {
                matrix[0][j] = 0;
            }
        }
        if (j0) {
            for (int i = 0; i < m; ++i) {
                matrix[i][0] = 0;
            }
        }
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
func setZeroes(matrix [][]int) {
    m, n := len(matrix), len(matrix[0])
    i0, j0 := false, false
    for j := 0; j < n; j++ {
        if matrix[0][j] == 0 {
            i0 = true
            break
        }
    }
    for i := 0; i < m; i++ {
        if matrix[i][0] == 0 {
            j0 = true
            break
        }
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n; j++ {
            if matrix[i][j] == 0 {
                matrix[i][0], matrix[0][j] = 0, 0
            }
        }
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n; j++ {
            if matrix[i][0] == 0 || matrix[0][j] == 0 {
                matrix[i][j] = 0
            }
        }
    }
    if i0 {
        for j := 0; j < n; j++ {
            matrix[0][j] = 0
        }
    }
    if j0 {
        for i := 0; i < m; i++ {
            matrix[i][0] = 0
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 Do not return anything, modify matrix in-place instead.
 */
function setZeroes(matrix: number[][]): void {
    const m = matrix.length;
    const n = matrix[0].length;
    const i0 = matrix[0].includes(0);
    const j0 = matrix.map(row => row[0]).includes(0);
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            if (matrix[i][j] === 0) {
                matrix[i][0] = 0;
                matrix[0][j] = 0;
            }
        }
    }
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            if (matrix[i][0] === 0 || matrix[0][j] === 0) {
                matrix[i][j] = 0;
            }
        }
    }
    if (i0) {
        matrix[0].fill(0);
    }
    if (j0) {
        for (let i = 0; i < m; ++i) {
            matrix[i][0] = 0;
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
var setZeroes = function (matrix) {
    const m = matrix.length;
    const n = matrix[0].length;
    let i0 = matrix[0].some(v => v == 0);
    let j0 = false;
    for (let i = 0; i < m; ++i) {
        if (matrix[i][0] == 0) {
            j0 = true;
            break;
        }
    }
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            if (matrix[i][j] == 0) {
                matrix[i][0] = 0;
                matrix[0][j] = 0;
            }
        }
    }
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                matrix[i][j] = 0;
            }
        }
    }
    if (i0) {
        for (let j = 0; j < n; ++j) {
            matrix[0][j] = 0;
        }
    }
    if (j0) {
        for (let i = 0; i < m; ++i) {
            matrix[i][0] = 0;
        }
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public class Solution {
    public void SetZeroes(int[][] matrix) {
        int m = matrix.Length, n = matrix[0].Length;
        bool i0 = matrix[0].Contains(0), j0 = false;
        for (int i = 0; i < m; ++i) {
            if (matrix[i][0] == 0) {
                j0 = true;
                break;
            }
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (i0) {
            for (int j = 0; j < n; ++j) {
                matrix[0][j] = 0;
            }
        }
        if (j0) {
            for (int i = 0; i < m; ++i) {
                matrix[i][0] = 0;
            }
        }
    }
}

评论