跳转至

723. 粉碎糖果 🔒

题目描述

这个问题是实现一个简单的消除算法。

给定一个 m x n 的二维整数数组 board 代表糖果所在的方格，不同的正整数 board[i][j] 代表不同种类的糖果，如果 board[i][j] == 0 代表 (i, j) 这个位置是空的。

给定的方格是玩家移动后的游戏状态，现在需要你根据以下规则粉碎糖果，使得整个方格处于稳定状态并最终输出：

  • 如果有三个及以上水平或者垂直相连的同种糖果，同一时间将它们粉碎，即将这些位置变成空的。
  • 在同时粉碎掉这些糖果之后，如果有一个空的位置上方还有糖果，那么上方的糖果就会下落直到碰到下方的糖果或者底部，这些糖果都是同时下落，也不会有新的糖果从顶部出现并落下来。
  • 通过前两步的操作，可能又会出现可以粉碎的糖果，请继续重复前面的操作。
  • 当不存在可以粉碎的糖果，也就是状态稳定之后，请输出最终的状态。

你需要模拟上述规则并使整个方格达到稳定状态，并输出。

 

示例 1 :

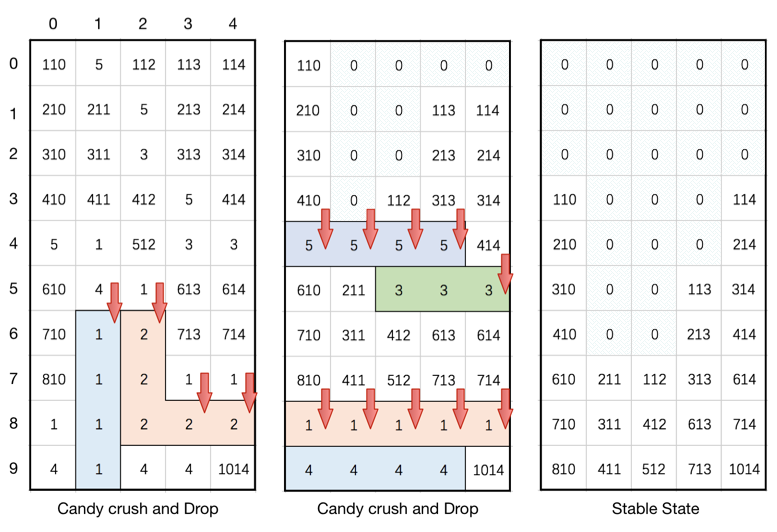
输入: board = [[110,5,112,113,114],[210,211,5,213,214],[310,311,3,313,314],[410,411,412,5,414],[5,1,512,3,3],[610,4,1,613,614],[710,1,2,713,714],[810,1,2,1,1],[1,1,2,2,2],[4,1,4,4,1014]]
输出: [[0,0,0,0,0],[0,0,0,0,0],[0,0,0,0,0],[110,0,0,0,114],[210,0,0,0,214],[310,0,0,113,314],[410,0,0,213,414],[610,211,112,313,614],[710,311,412,613,714],[810,411,512,713,1014]]

示例 2:

输入: board = [[1,3,5,5,2],[3,4,3,3,1],[3,2,4,5,2],[2,4,4,5,5],[1,4,4,1,1]]
输出: [[1,3,0,0,0],[3,4,0,5,2],[3,2,0,3,1],[2,4,0,5,2],[1,4,3,1,1]]

 

提示:

  • m == board.length
  • n == board[i].length
  • 3 <= m, n <= 50
  • 1 <= board[i][j] <= 2000

 

解法

方法一：模拟

我们可以逐行和逐列遍历矩阵，找到连续三个相同的元素，将它们标记为负数。如果成功标记，我们需要将矩阵中的元素下移，直到没有元素可以下移为止。

时间复杂度 $O(m^2 \times n^2)$，其中 $m$ 和 $n$ 分别是矩阵的行数和列数。空间复杂度 $O(1)$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
    def candyCrush(self, board: List[List[int]]) -> List[List[int]]:
        m, n = len(board), len(board[0])
        run = True
        while run:
            run = False
            for i in range(m):
                for j in range(2, n):
                    if board[i][j] and abs(board[i][j]) == abs(board[i][j - 1]) == abs(
                        board[i][j - 2]
                    ):
                        run = True
                        board[i][j] = board[i][j - 1] = board[i][j - 2] = -abs(
                            board[i][j]
                        )
            for j in range(n):
                for i in range(2, m):
                    if board[i][j] and abs(board[i][j]) == abs(board[i - 1][j]) == abs(
                        board[i - 2][j]
                    ):
                        run = True
                        board[i][j] = board[i - 1][j] = board[i - 2][j] = -abs(
                            board[i][j]
                        )
            if run:
                for j in range(n):
                    k = m - 1
                    for i in range(m - 1, -1, -1):
                        if board[i][j] > 0:
                            board[k][j] = board[i][j]
                            k -= 1
                    while k >= 0:
                        board[k][j] = 0
                        k -= 1
        return board

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    public int[][] candyCrush(int[][] board) {
        int m = board.length, n = board[0].length;
        boolean run = true;

        while (run) {
            run = false;
            for (int i = 0; i < m; i++) {
                for (int j = 2; j < n; j++) {
                    if (board[i][j] != 0 && Math.abs(board[i][j]) == Math.abs(board[i][j - 1])
                        && Math.abs(board[i][j]) == Math.abs(board[i][j - 2])) {
                        run = true;
                        int val = Math.abs(board[i][j]);
                        board[i][j] = board[i][j - 1] = board[i][j - 2] = -val;
                    }
                }
            }
            for (int j = 0; j < n; j++) {
                for (int i = 2; i < m; i++) {
                    if (board[i][j] != 0 && Math.abs(board[i][j]) == Math.abs(board[i - 1][j])
                        && Math.abs(board[i][j]) == Math.abs(board[i - 2][j])) {
                        run = true;
                        int val = Math.abs(board[i][j]);
                        board[i][j] = board[i - 1][j] = board[i - 2][j] = -val;
                    }
                }
            }
            if (run) {
                for (int j = 0; j < n; j++) {
                    int k = m - 1;
                    for (int i = m - 1; i >= 0; i--) {
                        if (board[i][j] > 0) {
                            board[k][j] = board[i][j];
                            k--;
                        }
                    }
                    while (k >= 0) {
                        board[k][j] = 0;
                        k--;
                    }
                }
            }
        }

        return board;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    vector<vector<int>> candyCrush(vector<vector<int>>& board) {
        int m = board.size(), n = board[0].size();
        bool run = true;
        while (run) {
            run = false;
            for (int i = 0; i < m; ++i) {
                for (int j = 0; j < n - 2; ++j) {
                    if (board[i][j] != 0 && abs(board[i][j]) == abs(board[i][j + 1]) && abs(board[i][j]) == abs(board[i][j + 2])) {
                        run = true;
                        board[i][j] = board[i][j + 1] = board[i][j + 2] = -abs(board[i][j]);
                    }
                }
            }
            for (int j = 0; j < n; ++j) {
                for (int i = 0; i < m - 2; ++i) {
                    if (board[i][j] != 0 && abs(board[i][j]) == abs(board[i + 1][j]) && abs(board[i][j]) == abs(board[i + 2][j])) {
                        run = true;
                        board[i][j] = board[i + 1][j] = board[i + 2][j] = -abs(board[i][j]);
                    }
                }
            }
            if (run) {
                for (int j = 0; j < n; ++j) {
                    int curr = m - 1;
                    for (int i = m - 1; i >= 0; --i) {
                        if (board[i][j] > 0) {
                            board[curr][j] = board[i][j];
                            --curr;
                        }
                    }
                    while (curr > -1) {
                        board[curr][j] = 0;
                        --curr;
                    }
                }
            }
        }
        return board;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
func candyCrush(board [][]int) [][]int {
    m := len(board)
    n := len(board[0])
    run := true

    for run {
        run = false
        for i := 0; i < m; i++ {
            for j := 2; j < n; j++ {
                if board[i][j] != 0 && abs(board[i][j]) == abs(board[i][j-1]) && abs(board[i][j]) == abs(board[i][j-2]) {
                    run = true
                    val := abs(board[i][j])
                    board[i][j] = -val
                    board[i][j-1] = -val
                    board[i][j-2] = -val
                }
            }
        }
        for j := 0; j < n; j++ {
            for i := 2; i < m; i++ {
                if board[i][j] != 0 && abs(board[i][j]) == abs(board[i-1][j]) && abs(board[i][j]) == abs(board[i-2][j]) {
                    run = true
                    val := abs(board[i][j])
                    board[i][j] = -val
                    board[i-1][j] = -val
                    board[i-2][j] = -val
                }
            }
        }
        if run {
            for j := 0; j < n; j++ {
                k := m - 1
                for i := m - 1; i >= 0; i-- {
                    if board[i][j] > 0 {
                        board[k][j] = board[i][j]
                        k--
                    }
                }
                for k >= 0 {
                    board[k][j] = 0
                    k--
                }
            }
        }
    }

    return board
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
function candyCrush(board: number[][]): number[][] {
    const m = board.length;
    const n = board[0].length;
    let run = true;
    while (run) {
        run = false;
        for (let i = 0; i < m; i++) {
            for (let j = 2; j < n; j++) {
                if (
                    board[i][j] !== 0 &&
                    Math.abs(board[i][j]) === Math.abs(board[i][j - 1]) &&
                    Math.abs(board[i][j]) === Math.abs(board[i][j - 2])
                ) {
                    run = true;
                    const val = Math.abs(board[i][j]);
                    board[i][j] = board[i][j - 1] = board[i][j - 2] = -val;
                }
            }
        }
        for (let j = 0; j < n; j++) {
            for (let i = 2; i < m; i++) {
                if (
                    board[i][j] !== 0 &&
                    Math.abs(board[i][j]) === Math.abs(board[i - 1][j]) &&
                    Math.abs(board[i][j]) === Math.abs(board[i - 2][j])
                ) {
                    run = true;
                    const val = Math.abs(board[i][j]);
                    board[i][j] = board[i - 1][j] = board[i - 2][j] = -val;
                }
            }
        }
        if (run) {
            for (let j = 0; j < n; j++) {
                let k = m - 1;
                for (let i = m - 1; i >= 0; i--) {
                    if (board[i][j] > 0) {
                        board[k][j] = board[i][j];
                        k--;
                    }
                }
                while (k >= 0) {
                    board[k][j] = 0;
                    k--;
                }
            }
        }
    }
    return board;
}

评论