
题目描述
对于一棵深度小于 5 的树,可以用一组三位十进制整数来表示。给定一个由三位数组成的 递增 的数组 nums 表示一棵深度小于 5 的二叉树,对于每个整数:
- 百位上的数字表示这个节点的深度
d,1 <= d <= 4。
- 十位上的数字表示这个节点在当前层所在的位置
p, 1 <= p <= 8。位置编号与一棵 满二叉树 的位置编号相同。
- 个位上的数字表示这个节点的权值
v,0 <= v <= 9。
返回从 根 到所有 叶子结点 的 路径 之 和。
保证 给定的数组表示一个有效的连接二叉树。
示例 1:
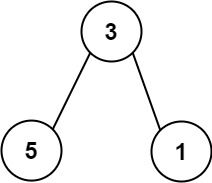
输入: nums = [113, 215, 221]
输出: 12
解释: 列表所表示的树如上所示。
路径和 = (3 + 5) + (3 + 1) = 12。
示例 2:
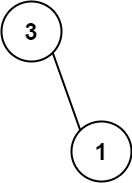
输入: nums = [113, 221]
输出: 4
解释: 列表所表示的树如上所示。
路径和 = (3 + 1) = 4。
提示:
1 <= nums.length <= 15110 <= nums[i] <= 489nums 表示深度小于 5 的有效二叉树nums 以升序排序。
解法
方法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution:
def pathSum(self, nums: List[int]) -> int:
def dfs(node, t):
if node not in mp:
return
t += mp[node]
d, p = divmod(node, 10)
l = (d + 1) * 10 + (p * 2) - 1
r = l + 1
nonlocal ans
if l not in mp and r not in mp:
ans += t
return
dfs(l, t)
dfs(r, t)
ans = 0
mp = {num // 10: num % 10 for num in nums}
dfs(11, 0)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | class Solution {
private int ans;
private Map<Integer, Integer> mp;
public int pathSum(int[] nums) {
ans = 0;
mp = new HashMap<>(nums.length);
for (int num : nums) {
mp.put(num / 10, num % 10);
}
dfs(11, 0);
return ans;
}
private void dfs(int node, int t) {
if (!mp.containsKey(node)) {
return;
}
t += mp.get(node);
int d = node / 10, p = node % 10;
int l = (d + 1) * 10 + (p * 2) - 1;
int r = l + 1;
if (!mp.containsKey(l) && !mp.containsKey(r)) {
ans += t;
return;
}
dfs(l, t);
dfs(r, t);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
public:
int ans;
unordered_map<int, int> mp;
int pathSum(vector<int>& nums) {
ans = 0;
mp.clear();
for (int num : nums) mp[num / 10] = num % 10;
dfs(11, 0);
return ans;
}
void dfs(int node, int t) {
if (!mp.count(node)) return;
t += mp[node];
int d = node / 10, p = node % 10;
int l = (d + 1) * 10 + (p * 2) - 1;
int r = l + 1;
if (!mp.count(l) && !mp.count(r)) {
ans += t;
return;
}
dfs(l, t);
dfs(r, t);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | func pathSum(nums []int) int {
ans := 0
mp := make(map[int]int)
for _, num := range nums {
mp[num/10] = num % 10
}
var dfs func(node, t int)
dfs = func(node, t int) {
if v, ok := mp[node]; ok {
t += v
d, p := node/10, node%10
l := (d+1)*10 + (p * 2) - 1
r := l + 1
if _, ok1 := mp[l]; !ok1 {
if _, ok2 := mp[r]; !ok2 {
ans += t
return
}
}
dfs(l, t)
dfs(r, t)
}
}
dfs(11, 0)
return ans
}
|


