跳转至

62. 不同路径

题目描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

 

示例 1：

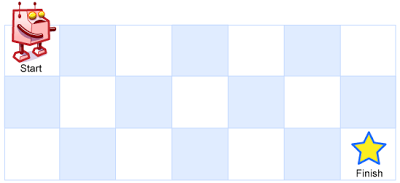
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

 

提示：

  • 1 <= m, n <= 100
  • 题目数据保证答案小于等于 2 * 109

解法

方法一：动态规划

我们定义 $f[i][j]$ 表示从左上角走到 $(i, j)$ 的路径数量，初始时 $f[0][0] = 1$，答案为 $f[m - 1][n - 1]$。

考虑 $f[i][j]$：

  • 如果 $i \gt 0$，那么 $f[i][j]$ 可以从 $f[i - 1][j]$ 走一步到达，因此 $f[i][j] = f[i][j] + f[i - 1][j]$；
  • 如果 $j \gt 0$，那么 $f[i][j]$ 可以从 $f[i][j - 1]$ 走一步到达，因此 $f[i][j] = f[i][j] + f[i][j - 1]$。

因此，我们有如下的状态转移方程：

$$ f[i][j] = \begin{cases} 1 & i = 0, j = 0 \ f[i - 1][j] + f[i][j - 1] & \textit{otherwise} \end{cases} $$

最终的答案即为 $f[m - 1][n - 1]$。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别是网格的行数和列数。

我们注意到 $f[i][j]$ 仅与 $f[i - 1][j]$ 和 $f[i][j - 1]$ 有关，因此我们优化掉第一维空间，仅保留第二维空间，得到时间复杂度 $O(m \times n)$，空间复杂度 $O(n)$ 的实现。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        f = [[0] * n for _ in range(m)]
        f[0][0] = 1
        for i in range(m):
            for j in range(n):
                if i:
                    f[i][j] += f[i - 1][j]
                if j:
                    f[i][j] += f[i][j - 1]
        return f[-1][-1]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
    public int uniquePaths(int m, int n) {
        var f = new int[m][n];
        f[0][0] = 1;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i > 0) {
                    f[i][j] += f[i - 1][j];
                }
                if (j > 0) {
                    f[i][j] += f[i][j - 1];
                }
            }
        }
        return f[m - 1][n - 1];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> f(m, vector<int>(n));
        f[0][0] = 1;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i) {
                    f[i][j] += f[i - 1][j];
                }
                if (j) {
                    f[i][j] += f[i][j - 1];
                }
            }
        }
        return f[m - 1][n - 1];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
func uniquePaths(m int, n int) int {
    f := make([][]int, m)
    for i := range f {
        f[i] = make([]int, n)
    }
    f[0][0] = 1
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if i > 0 {
                f[i][j] += f[i-1][j]
            }
            if j > 0 {
                f[i][j] += f[i][j-1]
            }
        }
    }
    return f[m-1][n-1]
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
function uniquePaths(m: number, n: number): number {
    const f: number[][] = Array(m)
        .fill(0)
        .map(() => Array(n).fill(0));
    f[0][0] = 1;
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (i > 0) {
                f[i][j] += f[i - 1][j];
            }
            if (j > 0) {
                f[i][j] += f[i][j - 1];
            }
        }
    }
    return f[m - 1][n - 1];
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
impl Solution {
    pub fn unique_paths(m: i32, n: i32) -> i32 {
        let (m, n) = (m as usize, n as usize);
        let mut f = vec![1; n];
        for i in 1..m {
            for j in 1..n {
                f[j] += f[j - 1];
            }
        }
        f[n - 1]
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function (m, n) {
    const f = Array(m)
        .fill(0)
        .map(() => Array(n).fill(0));
    f[0][0] = 1;
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (i > 0) {
                f[i][j] += f[i - 1][j];
            }
            if (j > 0) {
                f[i][j] += f[i][j - 1];
            }
        }
    }
    return f[m - 1][n - 1];
};

方法二

1
2
3
4
5
6
7
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        f = [[1] * n for _ in range(m)]
        for i in range(1, m):
            for j in range(1, n):
                f[i][j] = f[i - 1][j] + f[i][j - 1]
        return f[-1][-1]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution {
    public int uniquePaths(int m, int n) {
        var f = new int[m][n];
        for (var g : f) {
            Arrays.fill(g, 1);
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; j++) {
                f[i][j] = f[i - 1][j] + f[i][j - 1];
            }
        }
        return f[m - 1][n - 1];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> f(m, vector<int>(n, 1));
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[i][j] = f[i - 1][j] + f[i][j - 1];
            }
        }
        return f[m - 1][n - 1];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
func uniquePaths(m int, n int) int {
    f := make([][]int, m)
    for i := range f {
        f[i] = make([]int, n)
        for j := range f[i] {
            f[i][j] = 1
        }
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n; j++ {
            f[i][j] = f[i-1][j] + f[i][j-1]
        }
    }
    return f[m-1][n-1]
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
function uniquePaths(m: number, n: number): number {
    const f: number[][] = Array(m)
        .fill(0)
        .map(() => Array(n).fill(1));
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            f[i][j] = f[i - 1][j] + f[i][j - 1];
        }
    }
    return f[m - 1][n - 1];
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function (m, n) {
    const f = Array(m)
        .fill(0)
        .map(() => Array(n).fill(1));
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            f[i][j] = f[i - 1][j] + f[i][j - 1];
        }
    }
    return f[m - 1][n - 1];
};

方法三

1
2
3
4
5
6
7
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        f = [1] * n
        for _ in range(1, m):
            for j in range(1, n):
                f[j] += f[j - 1]
        return f[-1]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
    public int uniquePaths(int m, int n) {
        int[] f = new int[n];
        Arrays.fill(f, 1);
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[j] += f[j - 1];
            }
        }
        return f[n - 1];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> f(n, 1);
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[j] += f[j - 1];
            }
        }
        return f[n - 1];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
func uniquePaths(m int, n int) int {
    f := make([]int, n+1)
    for i := range f {
        f[i] = 1
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n; j++ {
            f[j] += f[j-1]
        }
    }
    return f[n-1]
}

1
2
3
4
5
6
7
8
9
function uniquePaths(m: number, n: number): number {
    const f: number[] = Array(n).fill(1);
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            f[j] += f[j - 1];
        }
    }
    return f[n - 1];
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function (m, n) {
    const f = Array(n).fill(1);
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            f[j] += f[j - 1];
        }
    }
    return f[n - 1];
};

评论