跳转至

598. 区间加法 II

题目描述

给你一个 m x n 的矩阵 M 和一个操作数组 op 。矩阵初始化时所有的单元格都为 0 。ops[i] = [ai, bi] 意味着当所有的 0 <= x < ai 和 0 <= y < bi 时， M[x][y] 应该加 1。

在 执行完所有操作后 ，计算并返回 矩阵中最大整数的个数 。

 

示例 1:

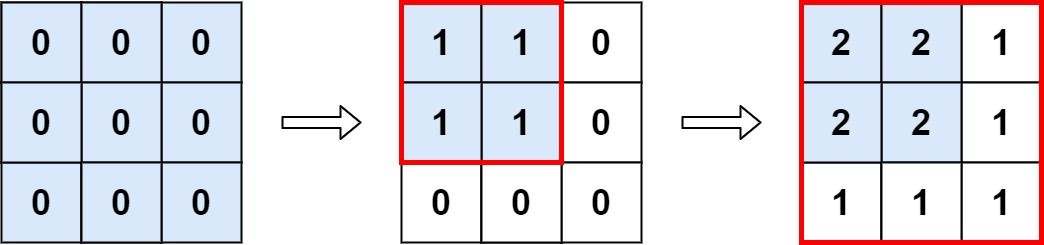
输入: m = 3, n = 3，ops = [[2,2],[3,3]]
输出: 4
解释: M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。

示例 2:

输入: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
输出: 4

示例 3:

输入: m = 3, n = 3, ops = []
输出: 9

 

提示:

  • 1 <= m, n <= 4 * 104
  • 0 <= ops.length <= 104
  • ops[i].length == 2
  • 1 <= ai <= m
  • 1 <= bi <= n

解法

方法一：脑筋急转弯

我们注意到，所有操作子矩阵的交集就是最终的最大整数所在的子矩阵，并且每个操作子矩阵都是从左上角 \((0, 0)\) 开始的，因此，我们遍历所有操作子矩阵，求出行数和列数的最小值，最后返回这两个值的乘积即可。

注意，如果操作数组为空，那么矩阵中的最大整数个数就是 \(m \times n\)。

时间复杂度 \(O(k)\)，其中 \(k\) 是操作数组 \(\textit{ops}\) 的长度。空间复杂度 \(O(1)\)。

1
2
3
4
5
6
class Solution:
    def maxCount(self, m: int, n: int, ops: List[List[int]]) -> int:
        for a, b in ops:
            m = min(m, a)
            n = min(n, b)
        return m * n

1
2
3
4
5
6
7
8
9
class Solution {
    public int maxCount(int m, int n, int[][] ops) {
        for (int[] op : ops) {
            m = Math.min(m, op[0]);
            n = Math.min(n, op[1]);
        }
        return m * n;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
class Solution {
public:
    int maxCount(int m, int n, vector<vector<int>>& ops) {
        for (auto op : ops) {
            m = min(m, op[0]);
            n = min(n, op[1]);
        }
        return m * n;
    }
};

1
2
3
4
5
6
7
func maxCount(m int, n int, ops [][]int) int {
    for _, op := range ops {
        m = min(m, op[0])
        n = min(n, op[1])
    }
    return m * n
}

1
2
3
4
5
6
7
function maxCount(m: number, n: number, ops: number[][]): number {
    for (const [a, b] of ops) {
        m = Math.min(m, a);
        n = Math.min(n, b);
    }
    return m * n;
}

1
2
3
4
5
6
7
8
9
impl Solution {
    pub fn max_count(mut m: i32, mut n: i32, ops: Vec<Vec<i32>>) -> i32 {
        for op in ops {
            m = m.min(op[0]);
            n = n.min(op[1]);
        }
        m * n
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
/**
 * @param {number} m
 * @param {number} n
 * @param {number[][]} ops
 * @return {number}
 */
var maxCount = function (m, n, ops) {
    for (const [a, b] of ops) {
        m = Math.min(m, a);
        n = Math.min(n, b);
    }
    return m * n;
};

评论