
题目描述
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
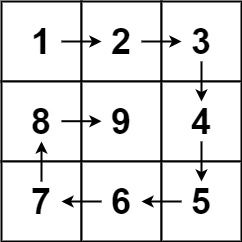
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
提示:
解法
方法一:模拟
我们可以直接模拟螺旋矩阵的生成过程。
定义一个二维数组 \(\textit{ans}\),用于存储螺旋矩阵。用 \(i\) 和 \(j\) 分别表示当前位置的行号和列号,用 \(k\) 表示当前的方向编号,\(\textit{dirs}\) 表示方向编号与方向的对应关系。
从 \(1\) 开始,依次填入矩阵中的每个位置。每次填入一个位置后,计算下一个位置的行号和列号,如果下一个位置不在矩阵中或者已经被填过,则改变方向,再计算下一个位置的行号和列号。
时间复杂度 \(O(n^2)\),其中 \(n\) 是矩阵的边长。忽略答案数组的空间消耗,空间复杂度 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12 | class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
ans = [[0] * n for _ in range(n)]
dirs = (0, 1, 0, -1, 0)
i = j = k = 0
for v in range(1, n * n + 1):
ans[i][j] = v
x, y = i + dirs[k], j + dirs[k + 1]
if x < 0 or x >= n or y < 0 or y >= n or ans[x][y]:
k = (k + 1) % 4
i, j = i + dirs[k], j + dirs[k + 1]
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution {
public int[][] generateMatrix(int n) {
int[][] ans = new int[n][n];
final int[] dirs = {0, 1, 0, -1, 0};
int i = 0, j = 0, k = 0;
for (int v = 1; v <= n * n; ++v) {
ans[i][j] = v;
int x = i + dirs[k], y = j + dirs[k + 1];
if (x < 0 || x >= n || y < 0 || y >= n || ans[x][y] != 0) {
k = (k + 1) % 4;
}
i += dirs[k];
j += dirs[k + 1];
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> ans(n, vector<int>(n, 0));
const int dirs[5] = {0, 1, 0, -1, 0};
int i = 0, j = 0, k = 0;
for (int v = 1; v <= n * n; ++v) {
ans[i][j] = v;
int x = i + dirs[k], y = j + dirs[k + 1];
if (x < 0 || x >= n || y < 0 || y >= n || ans[x][y] != 0) {
k = (k + 1) % 4;
}
i += dirs[k];
j += dirs[k + 1];
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | func generateMatrix(n int) [][]int {
ans := make([][]int, n)
for i := range ans {
ans[i] = make([]int, n)
}
dirs := [5]int{0, 1, 0, -1, 0}
i, j, k := 0, 0, 0
for v := 1; v <= n*n; v++ {
ans[i][j] = v
x, y := i+dirs[k], j+dirs[k+1]
if x < 0 || x >= n || y < 0 || y >= n || ans[x][y] != 0 {
k = (k + 1) % 4
}
i += dirs[k]
j += dirs[k+1]
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | function generateMatrix(n: number): number[][] {
const ans: number[][] = Array.from({ length: n }, () => Array(n).fill(0));
const dirs = [0, 1, 0, -1, 0];
let [i, j, k] = [0, 0, 0];
for (let v = 1; v <= n * n; v++) {
ans[i][j] = v;
const [x, y] = [i + dirs[k], j + dirs[k + 1]];
if (x < 0 || x >= n || y < 0 || y >= n || ans[x][y] !== 0) {
k = (k + 1) % 4;
}
i += dirs[k];
j += dirs[k + 1];
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | impl Solution {
pub fn generate_matrix(n: i32) -> Vec<Vec<i32>> {
let mut ans = vec![vec![0; n as usize]; n as usize];
let dirs = [0, 1, 0, -1, 0];
let (mut i, mut j, mut k) = (0, 0, 0);
for v in 1..=n * n {
ans[i as usize][j as usize] = v;
let (x, y) = (i + dirs[k], j + dirs[k + 1]);
if x < 0 || x >= n || y < 0 || y >= n || ans[x as usize][y as usize] != 0 {
k = (k + 1) % 4;
}
i += dirs[k];
j += dirs[k + 1];
}
ans
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | /**
* @param {number} n
* @return {number[][]}
*/
var generateMatrix = function (n) {
const ans = Array.from({ length: n }, () => Array(n).fill(0));
const dirs = [0, 1, 0, -1, 0];
let [i, j, k] = [0, 0, 0];
for (let v = 1; v <= n * n; v++) {
ans[i][j] = v;
const [x, y] = [i + dirs[k], j + dirs[k + 1]];
if (x < 0 || x >= n || y < 0 || y >= n || ans[x][y] !== 0) {
k = (k + 1) % 4;
}
i += dirs[k];
j += dirs[k + 1];
}
return ans;
};
|

