
题目描述
给定一个 m x n 的二进制矩阵 mat ,返回矩阵中最长的连续1线段。
这条线段可以是水平的、垂直的、对角线的或者反对角线的。
示例 1:
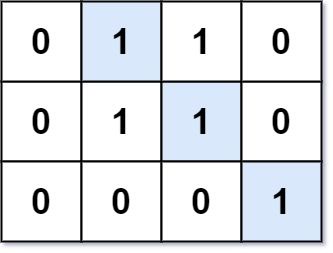
输入: mat = [[0,1,1,0],[0,1,1,0],[0,0,0,1]]
输出: 3
示例 2:
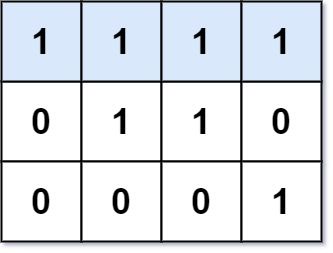
输入: mat = [[1,1,1,1],[0,1,1,0],[0,0,0,1]]
输出: 4
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j] 不是 0 就是 1.
解法
方法一:动态规划
我们定义 \(f[i][j][k]\) 表示方向为 \(k\),且以 \((i, j)\) 结尾的最长连续 \(1\) 的长度。其中 \(k\) 的取值范围为 \(0, 1, 2, 3\),分别表示水平、垂直、对角线、反对角线。
我们也可以用四个二维数组分别表示四个方向的最长连续 \(1\) 的长度。
遍历矩阵,当遇到 \(1\) 时,更新 \(f[i][j][k]\) 的值。对于每个位置 \((i, j)\),我们只需要更新其四个方向的值即可。然后更新答案。
时间复杂度 \(O(m \times n)\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别为矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution:
def longestLine(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0])
a = [[0] * (n + 2) for _ in range(m + 2)]
b = [[0] * (n + 2) for _ in range(m + 2)]
c = [[0] * (n + 2) for _ in range(m + 2)]
d = [[0] * (n + 2) for _ in range(m + 2)]
ans = 0
for i in range(1, m + 1):
for j in range(1, n + 1):
if mat[i - 1][j - 1]:
a[i][j] = a[i - 1][j] + 1
b[i][j] = b[i][j - 1] + 1
c[i][j] = c[i - 1][j - 1] + 1
d[i][j] = d[i - 1][j + 1] + 1
ans = max(ans, a[i][j], b[i][j], c[i][j], d[i][j])
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | class Solution {
public int longestLine(int[][] mat) {
int m = mat.length, n = mat[0].length;
int[][] a = new int[m + 2][n + 2];
int[][] b = new int[m + 2][n + 2];
int[][] c = new int[m + 2][n + 2];
int[][] d = new int[m + 2][n + 2];
int ans = 0;
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (mat[i - 1][j - 1] == 1) {
a[i][j] = a[i - 1][j] + 1;
b[i][j] = b[i][j - 1] + 1;
c[i][j] = c[i - 1][j - 1] + 1;
d[i][j] = d[i - 1][j + 1] + 1;
ans = max(ans, a[i][j], b[i][j], c[i][j], d[i][j]);
}
}
}
return ans;
}
private int max(int... arr) {
int ans = 0;
for (int v : arr) {
ans = Math.max(ans, v);
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution {
public:
int longestLine(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
vector<vector<int>> a(m + 2, vector<int>(n + 2));
vector<vector<int>> b(m + 2, vector<int>(n + 2));
vector<vector<int>> c(m + 2, vector<int>(n + 2));
vector<vector<int>> d(m + 2, vector<int>(n + 2));
int ans = 0;
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (mat[i - 1][j - 1]) {
a[i][j] = a[i - 1][j] + 1;
b[i][j] = b[i][j - 1] + 1;
c[i][j] = c[i - 1][j - 1] + 1;
d[i][j] = d[i - 1][j + 1] + 1;
ans = max(ans, max(a[i][j], max(b[i][j], max(c[i][j], d[i][j]))));
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | func longestLine(mat [][]int) (ans int) {
m, n := len(mat), len(mat[0])
f := make([][][4]int, m+2)
for i := range f {
f[i] = make([][4]int, n+2)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
if mat[i-1][j-1] == 1 {
f[i][j][0] = f[i-1][j][0] + 1
f[i][j][1] = f[i][j-1][1] + 1
f[i][j][2] = f[i-1][j-1][2] + 1
f[i][j][3] = f[i-1][j+1][3] + 1
for _, v := range f[i][j] {
if ans < v {
ans = v
}
}
}
}
}
return
}
|


