跳转至

536. 从字符串生成二叉树 🔒

题目描述

你需要用一个包括括号和整数的字符串构建一棵二叉树。

输入的字符串代表一棵二叉树。它包括整数和随后的 0 、1 或 2 对括号。整数代表根的值，一对括号内表示同样结构的子树。

若存在子结点，则从左子结点开始构建。

 

示例 1:

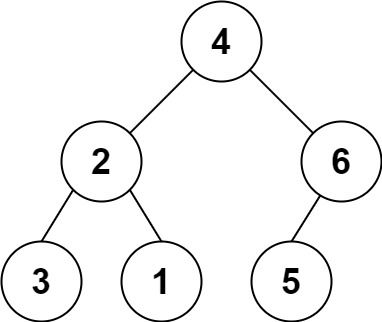
输入： s = "4(2(3)(1))(6(5))"
输出： [4,2,6,3,1,5]

示例 2:

输入： s = "4(2(3)(1))(6(5)(7))"
输出： [4,2,6,3,1,5,7]

示例 3:

输入： s = "-4(2(3)(1))(6(5)(7))"
输出： [-4,2,6,3,1,5,7]

 

提示：

  • 0 <= s.length <= 3 * 104
  • 输入字符串中只包含 '(', ')', '-' 和 '0' ~ '9' 
  • 空树由 "" 而非"()"表示。

解法

方法一

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def str2tree(self, s: str) -> TreeNode:
        def dfs(s):
            if not s:
                return None
            p = s.find('(')
            if p == -1:
                return TreeNode(int(s))
            root = TreeNode(int(s[:p]))
            start = p
            cnt = 0
            for i in range(p, len(s)):
                if s[i] == '(':
                    cnt += 1
                elif s[i] == ')':
                    cnt -= 1
                if cnt == 0:
                    if start == p:
                        root.left = dfs(s[start + 1 : i])
                        start = i + 1
                    else:
                        root.right = dfs(s[start + 1 : i])
            return root

        return dfs(s)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode str2tree(String s) {
        return dfs(s);
    }

    private TreeNode dfs(String s) {
        if ("".equals(s)) {
            return null;
        }
        int p = s.indexOf("(");
        if (p == -1) {
            return new TreeNode(Integer.parseInt(s));
        }
        TreeNode root = new TreeNode(Integer.parseInt(s.substring(0, p)));
        int start = p;
        int cnt = 0;
        for (int i = p; i < s.length(); ++i) {
            if (s.charAt(i) == '(') {
                ++cnt;
            } else if (s.charAt(i) == ')') {
                --cnt;
            }
            if (cnt == 0) {
                if (start == p) {
                    root.left = dfs(s.substring(start + 1, i));
                    start = i + 1;
                } else {
                    root.right = dfs(s.substring(start + 1, i));
                }
            }
        }
        return root;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* str2tree(string s) {
        return dfs(s);
    }

    TreeNode* dfs(string s) {
        if (s == "") return nullptr;
        int p = s.find("(");
        if (p == s.npos) return new TreeNode(stoi(s));
        TreeNode* root = new TreeNode(stoi(s.substr(0, p)));
        int start = p;
        int cnt = 0;
        for (int i = p; i < s.size(); ++i) {
            if (s[i] == '(')
                ++cnt;
            else if (s[i] == ')')
                --cnt;
            if (cnt == 0) {
                if (start == p) {
                    root->left = dfs(s.substr(start + 1, i - start - 1));
                    start = i + 1;
                } else
                    root->right = dfs(s.substr(start + 1, i - start - 1));
            }
        }
        return root;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func str2tree(s string) *TreeNode {
    var dfs func(s string) *TreeNode
    dfs = func(s string) *TreeNode {
        if s == "" {
            return nil
        }
        p := strings.IndexAny(s, "(")
        if p == -1 {
            v, _ := strconv.Atoi(s)
            return &TreeNode{Val: v}
        }
        v, _ := strconv.Atoi(s[:p])
        root := &TreeNode{Val: v}
        start := p
        cnt := 0
        for i := p; i < len(s); i++ {
            if s[i] == '(' {
                cnt++
            } else if s[i] == ')' {
                cnt--
            }
            if cnt == 0 {
                if p == start {
                    root.Left = dfs(s[start+1 : i])
                    start = i + 1
                } else {
                    root.Right = dfs(s[start+1 : i])
                }
            }
        }
        return root
    }
    return dfs(s)
}

评论