
题目描述
n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
示例 1:
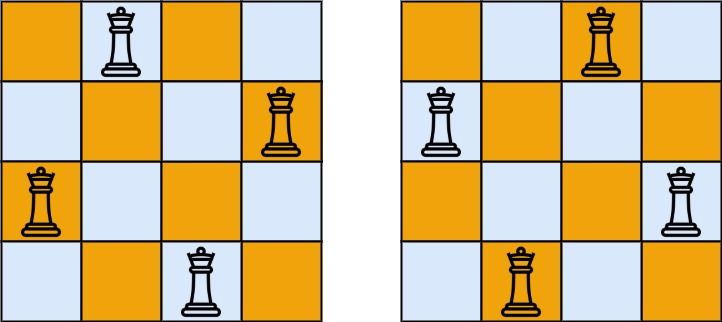
输入:n = 4
输出:2
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:1
提示:
解法
方法一:回溯
我们设计一个函数 \(dfs(i)\),表示从第 \(i\) 行开始搜索,搜索到的结果累加到答案中。
在第 \(i\) 行,我们枚举第 \(i\) 行的每一列,如果当前列不与前面已经放置的皇后发生冲突,那么我们就可以放置一个皇后,然后继续搜索下一行,即调用 \(dfs(i + 1)\)。
如果发生冲突,那么我们就跳过当前列,继续枚举下一列。
判断是否发生冲突,我们需要用三个数组分别记录每一列、每一条正对角线、每一条反对角线是否已经放置了皇后。
具体地,我们用 \(cols\) 数组记录每一列是否已经放置了皇后,用 \(dg\) 数组记录每一条正对角线是否已经放置了皇后,用 \(udg\) 数组记录每一条反对角线是否已经放置了皇后。
时间复杂度 \(O(n!)\),空间复杂度 \(O(n)\)。其中 \(n\) 是皇后的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution:
def totalNQueens(self, n: int) -> int:
def dfs(i: int):
if i == n:
nonlocal ans
ans += 1
return
for j in range(n):
a, b = i + j, i - j + n
if cols[j] or dg[a] or udg[b]:
continue
cols[j] = dg[a] = udg[b] = True
dfs(i + 1)
cols[j] = dg[a] = udg[b] = False
cols = [False] * 10
dg = [False] * 20
udg = [False] * 20
ans = 0
dfs(0)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | class Solution {
private int n;
private int ans;
private boolean[] cols = new boolean[10];
private boolean[] dg = new boolean[20];
private boolean[] udg = new boolean[20];
public int totalNQueens(int n) {
this.n = n;
dfs(0);
return ans;
}
private void dfs(int i) {
if (i == n) {
++ans;
return;
}
for (int j = 0; j < n; ++j) {
int a = i + j, b = i - j + n;
if (cols[j] || dg[a] || udg[b]) {
continue;
}
cols[j] = true;
dg[a] = true;
udg[b] = true;
dfs(i + 1);
cols[j] = false;
dg[a] = false;
udg[b] = false;
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | class Solution {
public:
int totalNQueens(int n) {
bitset<10> cols;
bitset<20> dg;
bitset<20> udg;
int ans = 0;
function<void(int)> dfs = [&](int i) {
if (i == n) {
++ans;
return;
}
for (int j = 0; j < n; ++j) {
int a = i + j, b = i - j + n;
if (cols[j] || dg[a] || udg[b]) continue;
cols[j] = dg[a] = udg[b] = 1;
dfs(i + 1);
cols[j] = dg[a] = udg[b] = 0;
}
};
dfs(0);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | func totalNQueens(n int) (ans int) {
cols := [10]bool{}
dg := [20]bool{}
udg := [20]bool{}
var dfs func(int)
dfs = func(i int) {
if i == n {
ans++
return
}
for j := 0; j < n; j++ {
a, b := i+j, i-j+n
if cols[j] || dg[a] || udg[b] {
continue
}
cols[j], dg[a], udg[b] = true, true, true
dfs(i + 1)
cols[j], dg[a], udg[b] = false, false, false
}
}
dfs(0)
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | function totalNQueens(n: number): number {
const cols: boolean[] = Array(10).fill(false);
const dg: boolean[] = Array(20).fill(false);
const udg: boolean[] = Array(20).fill(false);
let ans = 0;
const dfs = (i: number) => {
if (i === n) {
++ans;
return;
}
for (let j = 0; j < n; ++j) {
let [a, b] = [i + j, i - j + n];
if (cols[j] || dg[a] || udg[b]) {
continue;
}
cols[j] = dg[a] = udg[b] = true;
dfs(i + 1);
cols[j] = dg[a] = udg[b] = false;
}
};
dfs(0);
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | function totalNQueens(n) {
const cols = Array(10).fill(false);
const dg = Array(20).fill(false);
const udg = Array(20).fill(false);
let ans = 0;
const dfs = i => {
if (i === n) {
++ans;
return;
}
for (let j = 0; j < n; ++j) {
let [a, b] = [i + j, i - j + n];
if (cols[j] || dg[a] || udg[b]) {
continue;
}
cols[j] = dg[a] = udg[b] = true;
dfs(i + 1);
cols[j] = dg[a] = udg[b] = false;
}
};
dfs(0);
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | public class Solution {
public int TotalNQueens(int n) {
bool[] cols = new bool[10];
bool[] dg = new bool[20];
bool[] udg = new bool[20];
int ans = 0;
void dfs(int i) {
if (i == n) {
ans++;
return;
}
for (int j = 0; j < n; j++) {
int a = i + j, b = i - j + n;
if (cols[j] || dg[a] || udg[b]) {
continue;
}
cols[j] = dg[a] = udg[b] = true;
dfs(i + 1);
cols[j] = dg[a] = udg[b] = false;
}
}
dfs(0);
return ans;
}
}
|

