
题目描述
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
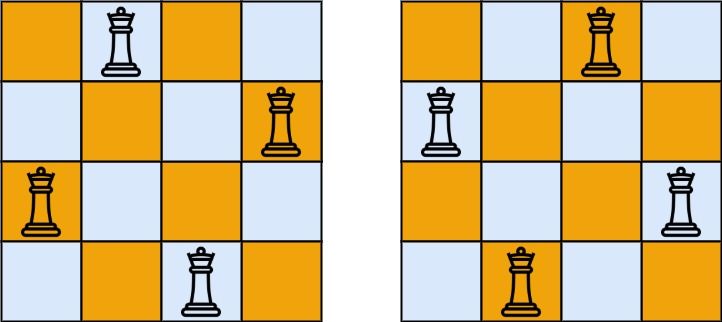
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
提示:
解法
方法一:DFS(回溯)
我们定义三个数组 \(col\), \(dg\) 和 \(udg\),分别表示列、正对角线和反对角线上的是否有皇后,如果位置 \((i, j)\) 有皇后,那么 \(col[j]\), \(dg[i + j]\) 和 \(udg[n - i + j]\) 都为 \(1\)。另外,我们用一个数组 \(g\) 记录当前棋盘的状态,初始时 \(g\) 中的所有元素都是 '.'。
接下来,我们定义一个函数 \(dfs(i)\),表示从第 \(i\) 行开始放置皇后。
在 \(dfs(i)\) 中,如果 \(i=n\),说明我们已经完成了所有皇后的放置,我们将当前 \(g\) 放入答案数组中,递归结束。
否则,我们枚举当前行的每一列 \(j\),如果位置 \((i, j)\) 没有皇后,即 \(col[j]\), \(dg[i + j]\) 和 \(udg[n - i + j]\) 都为 \(0\),那么我们可以放置皇后,即把 \(g[i][j]\) 改为 'Q',并将 \(col[j]\), \(dg[i + j]\) 和 \(udg[n - i + j]\) 都置为 \(1\),然后继续搜索下一行,即调用 \(dfs(i + 1)\),递归结束后,我们需要将 \(g[i][j]\) 改回 '.' 并将 \(col[j]\), \(dg[i + j]\) 和 \(udg[n - i + j]\) 都置为 \(0\)。
在主函数中,我们调用 \(dfs(0)\) 开始递归,最后返回答案数组即可。
时间复杂度 \((n^2 \times n!)\),空间复杂度 \(O(n)\)。其中 \(n\) 是题目给定的整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
def dfs(i: int):
if i == n:
ans.append(["".join(row) for row in g])
return
for j in range(n):
if col[j] + dg[i + j] + udg[n - i + j] == 0:
g[i][j] = "Q"
col[j] = dg[i + j] = udg[n - i + j] = 1
dfs(i + 1)
col[j] = dg[i + j] = udg[n - i + j] = 0
g[i][j] = "."
ans = []
g = [["."] * n for _ in range(n)]
col = [0] * n
dg = [0] * (n << 1)
udg = [0] * (n << 1)
dfs(0)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | class Solution {
private List<List<String>> ans = new ArrayList<>();
private int[] col;
private int[] dg;
private int[] udg;
private String[][] g;
private int n;
public List<List<String>> solveNQueens(int n) {
this.n = n;
col = new int[n];
dg = new int[n << 1];
udg = new int[n << 1];
g = new String[n][n];
for (int i = 0; i < n; ++i) {
Arrays.fill(g[i], ".");
}
dfs(0);
return ans;
}
private void dfs(int i) {
if (i == n) {
List<String> t = new ArrayList<>();
for (int j = 0; j < n; ++j) {
t.add(String.join("", g[j]));
}
ans.add(t);
return;
}
for (int j = 0; j < n; ++j) {
if (col[j] + dg[i + j] + udg[n - i + j] == 0) {
g[i][j] = "Q";
col[j] = dg[i + j] = udg[n - i + j] = 1;
dfs(i + 1);
col[j] = dg[i + j] = udg[n - i + j] = 0;
g[i][j] = ".";
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
vector<int> col(n);
vector<int> dg(n << 1);
vector<int> udg(n << 1);
vector<vector<string>> ans;
vector<string> t(n, string(n, '.'));
function<void(int)> dfs = [&](int i) -> void {
if (i == n) {
ans.push_back(t);
return;
}
for (int j = 0; j < n; ++j) {
if (col[j] + dg[i + j] + udg[n - i + j] == 0) {
t[i][j] = 'Q';
col[j] = dg[i + j] = udg[n - i + j] = 1;
dfs(i + 1);
col[j] = dg[i + j] = udg[n - i + j] = 0;
t[i][j] = '.';
}
}
};
dfs(0);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | func solveNQueens(n int) (ans [][]string) {
col := make([]int, n)
dg := make([]int, n<<1)
udg := make([]int, n<<1)
t := make([][]byte, n)
for i := range t {
t[i] = make([]byte, n)
for j := range t[i] {
t[i][j] = '.'
}
}
var dfs func(int)
dfs = func(i int) {
if i == n {
tmp := make([]string, n)
for i := range tmp {
tmp[i] = string(t[i])
}
ans = append(ans, tmp)
return
}
for j := 0; j < n; j++ {
if col[j]+dg[i+j]+udg[n-i+j] == 0 {
col[j], dg[i+j], udg[n-i+j] = 1, 1, 1
t[i][j] = 'Q'
dfs(i + 1)
t[i][j] = '.'
col[j], dg[i+j], udg[n-i+j] = 0, 0, 0
}
}
}
dfs(0)
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | function solveNQueens(n: number): string[][] {
const col: number[] = Array(n).fill(0);
const dg: number[] = Array(n << 1).fill(0);
const udg: number[] = Array(n << 1).fill(0);
const ans: string[][] = [];
const t: string[][] = Array.from({ length: n }, () => Array(n).fill('.'));
const dfs = (i: number) => {
if (i === n) {
ans.push(t.map(x => x.join('')));
return;
}
for (let j = 0; j < n; ++j) {
if (col[j] + dg[i + j] + udg[n - i + j] === 0) {
t[i][j] = 'Q';
col[j] = dg[i + j] = udg[n - i + j] = 1;
dfs(i + 1);
col[j] = dg[i + j] = udg[n - i + j] = 0;
t[i][j] = '.';
}
}
};
dfs(0);
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | public class Solution {
private int n;
private int[] col;
private int[] dg;
private int[] udg;
private IList<IList<string>> ans = new List<IList<string>>();
private IList<string> t = new List<string>();
public IList<IList<string>> SolveNQueens(int n) {
this.n = n;
col = new int[n];
dg = new int[n << 1];
udg = new int[n << 1];
dfs(0);
return ans;
}
private void dfs(int i) {
if (i == n) {
ans.Add(new List<string>(t));
return;
}
for (int j = 0; j < n; ++j) {
if (col[j] + dg[i + j] + udg[n - i + j] == 0) {
char[] row = new char[n];
Array.Fill(row, '.');
row[j] = 'Q';
t.Add(new string(row));
col[j] = dg[i + j] = udg[n - i + j] = 1;
dfs(i + 1);
col[j] = dg[i + j] = udg[n - i + j] = 0;
t.RemoveAt(t.Count - 1);
}
}
}
}
|

