二叉搜索树
二叉树
树
深度优先搜索
题目描述
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数 (即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树
示例 1:
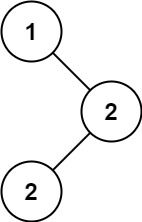
输入: root = [1,null,2,2]
输出: [2]
示例 2:
输入: root = [0]
输出: [0]
提示:
树中节点的数目在范围 [1, 104 ] 内
-105 <= Node.val <= 105
进阶: 你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
解法
方法一
Python3 Java C++ Go C#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def findMode ( self , root : TreeNode ) -> List [ int ]:
def dfs ( root ):
if root is None :
return
nonlocal mx , prev , ans , cnt
dfs ( root . left )
cnt = cnt + 1 if prev == root . val else 1
if cnt > mx :
ans = [ root . val ]
mx = cnt
elif cnt == mx :
ans . append ( root . val )
prev = root . val
dfs ( root . right )
prev = None
mx = cnt = 0
ans = []
dfs ( root )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int mx ;
private int cnt ;
private TreeNode prev ;
private List < Integer > res ;
public int [] findMode ( TreeNode root ) {
res = new ArrayList <> ();
dfs ( root );
int [] ans = new int [ res . size () ] ;
for ( int i = 0 ; i < res . size (); ++ i ) {
ans [ i ] = res . get ( i );
}
return ans ;
}
private void dfs ( TreeNode root ) {
if ( root == null ) {
return ;
}
dfs ( root . left );
cnt = prev != null && prev . val == root . val ? cnt + 1 : 1 ;
if ( cnt > mx ) {
res = new ArrayList <> ( Arrays . asList ( root . val ));
mx = cnt ;
} else if ( cnt == mx ) {
res . add ( root . val );
}
prev = root ;
dfs ( root . right );
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
TreeNode * prev ;
int mx , cnt ;
vector < int > ans ;
vector < int > findMode ( TreeNode * root ) {
dfs ( root );
return ans ;
}
void dfs ( TreeNode * root ) {
if ( ! root ) return ;
dfs ( root -> left );
cnt = prev != nullptr && prev -> val == root -> val ? cnt + 1 : 1 ;
if ( cnt > mx ) {
ans . clear ();
ans . push_back ( root -> val );
mx = cnt ;
} else if ( cnt == mx )
ans . push_back ( root -> val );
prev = root ;
dfs ( root -> right );
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func findMode ( root * TreeNode ) [] int {
mx , cnt := 0 , 0
var prev * TreeNode
var ans [] int
var dfs func ( root * TreeNode )
dfs = func ( root * TreeNode ) {
if root == nil {
return
}
dfs ( root . Left )
if prev != nil && prev . Val == root . Val {
cnt ++
} else {
cnt = 1
}
if cnt > mx {
ans = [] int { root . Val }
mx = cnt
} else if cnt == mx {
ans = append ( ans , root . Val )
}
prev = root
dfs ( root . Right )
}
dfs ( root )
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 public class Solution {
private int mx ;
private int cnt ;
private TreeNode prev ;
private List < int > res ;
public int [] FindMode ( TreeNode root ) {
res = new List < int > ();
Dfs ( root );
int [] ans = new int [ res . Count ];
for ( int i = 0 ; i < res . Count ; ++ i ) {
ans [ i ] = res [ i ];
}
return ans ;
}
private void Dfs ( TreeNode root ) {
if ( root == null ) {
return ;
}
Dfs ( root . left );
cnt = prev != null && prev . val == root . val ? cnt + 1 : 1 ;
if ( cnt > mx ) {
res = new List < int > ( new int [] { root . val });
mx = cnt ;
} else if ( cnt == mx ) {
res . Add ( root . val );
}
prev = root ;
Dfs ( root . right );
}
}
GitHub