跳转至

48. 旋转图像

题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

 

示例 1：

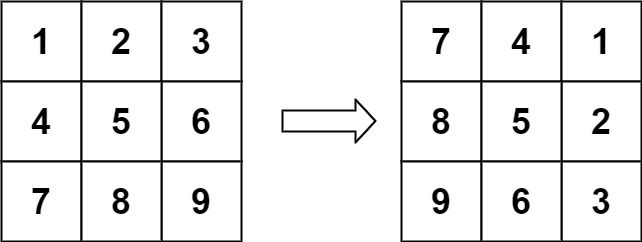
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

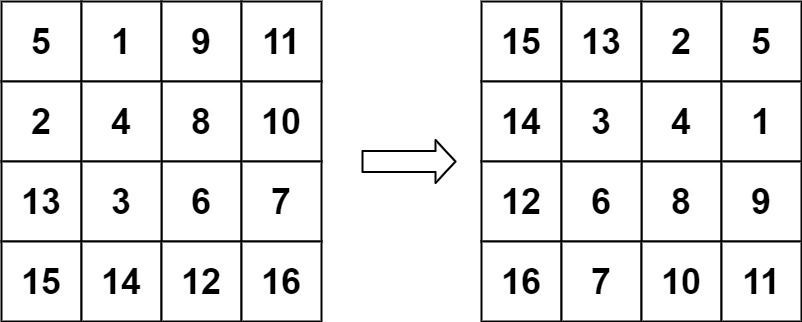
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

 

提示：

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 20
  • -1000 <= matrix[i][j] <= 1000

 

解法

方法一：原地翻转

根据题目要求，我们实际上需要将 $matrix[i][j]$ 旋转至 $matrix[j][n - i - 1]$。

我们可以先对矩阵进行上下翻转，即 $matrix[i][j]$ 和 $matrix[n - i - 1][j]$ 进行交换，然后再对矩阵进行主对角线翻转，即 $matrix[i][j]$ 和 $matrix[j][i]$ 进行交换。这样就能将 $matrix[i][j]$ 旋转至 $matrix[j][n - i - 1]$ 了。

时间复杂度 $O(n^2)$，其中 $n$ 是矩阵的边长。空间复杂度 $O(1)$。

1
2
3
4
5
6
7
8
9
class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        for i in range(n >> 1):
            for j in range(n):
                matrix[i][j], matrix[n - i - 1][j] = matrix[n - i - 1][j], matrix[i][j]
        for i in range(n):
            for j in range(i):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n >> 1; ++i) {
            for (int j = 0; j < n; ++j) {
                int t = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = t;
            }
        }
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                int t = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = t;
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n >> 1; ++i) {
            for (int j = 0; j < n; ++j) {
                swap(matrix[i][j], matrix[n - i - 1][j]);
            }
        }
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
func rotate(matrix [][]int) {
    n := len(matrix)
    for i := 0; i < n>>1; i++ {
        for j := 0; j < n; j++ {
            matrix[i][j], matrix[n-i-1][j] = matrix[n-i-1][j], matrix[i][j]
        }
    }
    for i := 0; i < n; i++ {
        for j := 0; j < i; j++ {
            matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
/**
 Do not return anything, modify matrix in-place instead.
 */
function rotate(matrix: number[][]): void {
    matrix.reverse();
    for (let i = 0; i < matrix.length; ++i) {
        for (let j = 0; j < i; ++j) {
            const t = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = t;
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
impl Solution {
    pub fn rotate(matrix: &mut Vec<Vec<i32>>) {
        let n = matrix.len();
        for i in 0..n / 2 {
            for j in 0..n {
                let t = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = t;
            }
        }
        for i in 0..n {
            for j in 0..i {
                let t = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = t;
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
var rotate = function (matrix) {
    matrix.reverse();
    for (let i = 0; i < matrix.length; ++i) {
        for (let j = 0; j < i; ++j) {
            [matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
        }
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
public class Solution {
    public void Rotate(int[][] matrix) {
        int n = matrix.Length;
        for (int i = 0; i < n >> 1; ++i) {
            for (int j = 0; j < n; ++j) {
                int t = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = t;
            }
        }
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                int t = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = t;
            }
        }
    }
}

评论