
题目描述
我们都知道安卓有个手势解锁的界面,是一个 3 x 3 的点所绘制出来的网格。用户可以设置一个 “解锁模式” ,通过连接特定序列中的点,形成一系列彼此连接的线段,每个线段的端点都是序列中两个连续的点。如果满足以下两个条件,则 k 点序列是有效的解锁模式:
- 解锁模式中的所有点 互不相同 。
- 假如模式中两个连续点的线段需要经过其他点的 中心 ,那么要经过的点 必须提前出现 在序列中(已经经过),不能跨过任何还未被经过的点。
- 例如,点
5 或 6 没有提前出现的情况下连接点 2 和 9 是有效的,因为从点 2 到点 9 的线没有穿过点 5 或 6 的中心。
- 然而,点
2 没有提前出现的情况下连接点 1 和 3 是无效的,因为从圆点 1 到圆点 3 的直线穿过圆点 2 的中心。
以下是一些有效和无效解锁模式的示例:
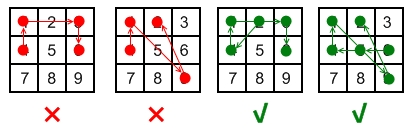
- 无效手势:
[4,1,3,6] ,连接点 1 和点 3 时经过了未被连接过的 2 号点。
- 无效手势:
[4,1,9,2] ,连接点 1 和点 9 时经过了未被连接过的 5 号点。
- 有效手势:
[2,4,1,3,6] ,连接点 1 和点 3 是有效的,因为虽然它经过了点 2 ,但是点 2 在该手势中之前已经被连过了。
- 有效手势:
[6,5,4,1,9,2] ,连接点 1 和点 9 是有效的,因为虽然它经过了按键 5 ,但是点 5 在该手势中之前已经被连过了。
给你两个整数,分别为 m 和 n ,那么请返回有多少种 不同且有效的解锁模式 ,是 至少 需要经过 m 个点,但是 不超过 n 个点的。
两个解锁模式 不同 需满足:经过的点不同或者经过点的顺序不同。
示例 1:
输入:m = 1, n = 1
输出:9
示例 2:
输入:m = 1, n = 2
输出:65
提示:
解法
方法一:DFS
我们定义一个二维数组 \(cross\),其中 \(cross[i][j]\) 表示数字 \(i\) 和数字 \(j\) 之间是否有中间数字,如果有则 \(cross[i][j]\) 的值为中间数字,否则为 \(0\)。
我们还需要一个一维数组 \(vis\),用来记录数字是否被使用过。
由于数字 \(1\), \(3\), \(7\), \(9\) 是对称的,因此我们只需要计算数字 \(1\) 的情况,然后乘以 \(4\) 即可。
由于数字 \(2\), \(4\), \(6\), \(8\) 也是对称的,因此我们只需要计算数字 \(2\) 的情况,然后乘以 \(4\) 即可。
最后我们再计算数字 \(5\) 的情况。
我们设计一个函数 \(dfs(i, cnt)\),表示当前位于数字 \(i\),且已经选了 \(cnt\) 个数字的情况下,有多少种解锁模式。
函数 \(dfs(i, cnt)\) 的执行过程如下:
如果 \(cnt \gt n\),说明当前选中的数字个数超过了 \(n\),直接返回 \(0\)。
否则,我们将数字 \(i\) 标记为已使用,然后初始化答案 \(ans\) 为 \(0\)。如果 \(cnt \ge m\),说明当前选中的数字个数不少于 \(m\),那么答案 \(ans\) 就需要加 \(1\)。
接下来,我们枚举下一个数字 \(j\),如果数字 \(j\) 没有被使用过,且数字 \(i\) 和数字 \(j\) 之间没有中间数字,或者数字 \(i\) 和数字 \(j\) 之间的中间数字已经被使用过,那么我们就可以从数字 \(j\) 出发,继续搜索,此时答案 \(ans\) 需要加上 \(dfs(j, cnt + 1)\) 的返回值。
最后,我们将数字 \(i\) 标记为未使用,然后返回答案 \(ans\)。
最终的答案即为 \(dfs(1, 1) \times 4 + dfs(2, 1) \times 4 + dfs(5, 1)\)。
时间复杂度 \(O(n!)\),空间复杂度 \(O(n)\)。其中 \(n\) 是手势的最大长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | class Solution:
def numberOfPatterns(self, m: int, n: int) -> int:
def dfs(i: int, cnt: int = 1) -> int:
if cnt > n:
return 0
vis[i] = True
ans = int(cnt >= m)
for j in range(1, 10):
x = cross[i][j]
if not vis[j] and (x == 0 or vis[x]):
ans += dfs(j, cnt + 1)
vis[i] = False
return ans
cross = [[0] * 10 for _ in range(10)]
cross[1][3] = cross[3][1] = 2
cross[1][7] = cross[7][1] = 4
cross[1][9] = cross[9][1] = 5
cross[2][8] = cross[8][2] = 5
cross[3][7] = cross[7][3] = 5
cross[3][9] = cross[9][3] = 6
cross[4][6] = cross[6][4] = 5
cross[7][9] = cross[9][7] = 8
vis = [False] * 10
return dfs(1) * 4 + dfs(2) * 4 + dfs(5)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | class Solution {
private int m;
private int n;
private int[][] cross = new int[10][10];
private boolean[] vis = new boolean[10];
public int numberOfPatterns(int m, int n) {
this.m = m;
this.n = n;
cross[1][3] = cross[3][1] = 2;
cross[1][7] = cross[7][1] = 4;
cross[1][9] = cross[9][1] = 5;
cross[2][8] = cross[8][2] = 5;
cross[3][7] = cross[7][3] = 5;
cross[3][9] = cross[9][3] = 6;
cross[4][6] = cross[6][4] = 5;
cross[7][9] = cross[9][7] = 8;
return dfs(1, 1) * 4 + dfs(2, 1) * 4 + dfs(5, 1);
}
private int dfs(int i, int cnt) {
if (cnt > n) {
return 0;
}
vis[i] = true;
int ans = cnt >= m ? 1 : 0;
for (int j = 1; j < 10; ++j) {
int x = cross[i][j];
if (!vis[j] && (x == 0 || vis[x])) {
ans += dfs(j, cnt + 1);
}
}
vis[i] = false;
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | class Solution {
public:
int numberOfPatterns(int m, int n) {
int cross[10][10];
memset(cross, 0, sizeof(cross));
bool vis[10];
memset(vis, false, sizeof(vis));
cross[1][3] = cross[3][1] = 2;
cross[1][7] = cross[7][1] = 4;
cross[1][9] = cross[9][1] = 5;
cross[2][8] = cross[8][2] = 5;
cross[3][7] = cross[7][3] = 5;
cross[3][9] = cross[9][3] = 6;
cross[4][6] = cross[6][4] = 5;
cross[7][9] = cross[9][7] = 8;
function<int(int, int)> dfs = [&](int i, int cnt) {
if (cnt > n) {
return 0;
}
vis[i] = true;
int ans = cnt >= m ? 1 : 0;
for (int j = 1; j < 10; ++j) {
int x = cross[i][j];
if (!vis[j] && (x == 0 || vis[x])) {
ans += dfs(j, cnt + 1);
}
}
vis[i] = false;
return ans;
};
return dfs(1, 1) * 4 + dfs(2, 1) * 4 + dfs(5, 1);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | func numberOfPatterns(m int, n int) int {
cross := [10][10]int{}
vis := [10]bool{}
cross[1][3] = 2
cross[1][7] = 4
cross[1][9] = 5
cross[2][8] = 5
cross[3][7] = 5
cross[3][9] = 6
cross[4][6] = 5
cross[7][9] = 8
cross[3][1] = 2
cross[7][1] = 4
cross[9][1] = 5
cross[8][2] = 5
cross[7][3] = 5
cross[9][3] = 6
cross[6][4] = 5
cross[9][7] = 8
var dfs func(int, int) int
dfs = func(i, cnt int) int {
if cnt > n {
return 0
}
vis[i] = true
ans := 0
if cnt >= m {
ans++
}
for j := 1; j < 10; j++ {
x := cross[i][j]
if !vis[j] && (x == 0 || vis[x]) {
ans += dfs(j, cnt+1)
}
}
vis[i] = false
return ans
}
return dfs(1, 1)*4 + dfs(2, 1)*4 + dfs(5, 1)
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | function numberOfPatterns(m: number, n: number): number {
const cross: number[][] = Array(10)
.fill(0)
.map(() => Array(10).fill(0));
const vis: boolean[] = Array(10).fill(false);
cross[1][3] = cross[3][1] = 2;
cross[1][7] = cross[7][1] = 4;
cross[1][9] = cross[9][1] = 5;
cross[2][8] = cross[8][2] = 5;
cross[3][7] = cross[7][3] = 5;
cross[3][9] = cross[9][3] = 6;
cross[4][6] = cross[6][4] = 5;
cross[7][9] = cross[9][7] = 8;
const dfs = (i: number, cnt: number): number => {
if (cnt > n) {
return 0;
}
vis[i] = true;
let ans = 0;
if (cnt >= m) {
++ans;
}
for (let j = 1; j < 10; ++j) {
const x = cross[i][j];
if (!vis[j] && (x === 0 || vis[x])) {
ans += dfs(j, cnt + 1);
}
}
vis[i] = false;
return ans;
};
return dfs(1, 1) * 4 + dfs(2, 1) * 4 + dfs(5, 1);
}
|

