跳转至

3402. 使每一列严格递增的最少操作次数

题目描述

给你一个由 非负 整数组成的 m x n 矩阵 grid。

在一次操作中，你可以将任意元素 grid[i][j] 的值增加 1。

返回使 grid 的所有列 严格递增 所需的 最少 操作次数。

 

示例 1：

输入: grid = [[3,2],[1,3],[3,4],[0,1]]

输出: 15

解释:

  • 为了让第 0 列严格递增，可以对 grid[1][0] 执行 3 次操作，对 grid[2][0] 执行 2 次操作，对 grid[3][0] 执行 6 次操作。
  • 为了让第 1 列严格递增，可以对 grid[3][1] 执行 4 次操作。

示例 2：

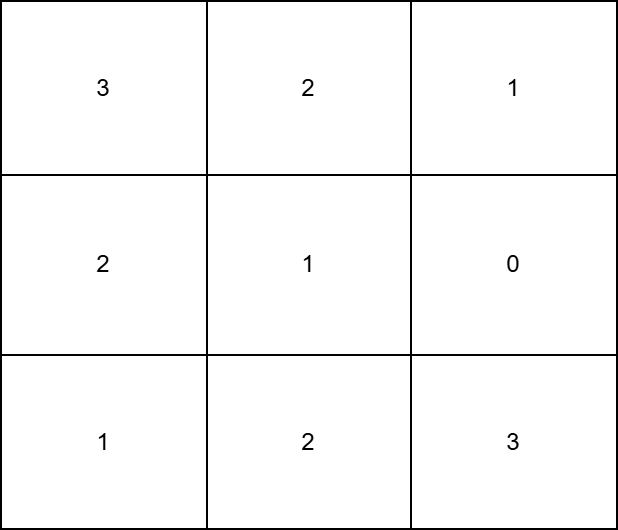
输入: grid = [[3,2,1],[2,1,0],[1,2,3]]

输出: 12

解释:

  • 为了让第 0 列严格递增，可以对 grid[1][0] 执行 2 次操作，对 grid[2][0] 执行 4 次操作。
  • 为了让第 1 列严格递增，可以对 grid[1][1] 执行 2 次操作，对 grid[2][1] 执行 2 次操作。
  • 为了让第 2 列严格递增，可以对 grid[1][2] 执行 2 次操作。

 

提示:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 50
  • 0 <= grid[i][j] < 2500

解法

方法一：逐列计算

我们可以逐列遍历矩阵，对于每一列，我们可以计算出使其严格递增所需的最少操作次数。具体地，对于每一列，我们可以维护一个变量 $\textit{pre}$，表示当前列中前一个元素的值。然后，我们从上到下遍历当前列，对于当前元素 $\textit{cur}$，如果 $\textit{pre} < \textit{cur}$，则说明当前元素已经大于前一个元素，我们只需要更新 $\textit{pre} = \textit{cur}$；否则，我们需要将当前元素增加到 $\textit{pre} + 1$，并将增加的次数累加到答案中。

时间复杂度 $O(m \times n)$，其中 $m$ 和 $n$ 分别是矩阵 $\textit{grid}$ 的行数和列数。空间复杂度 $O(1)$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution:
    def minimumOperations(self, grid: List[List[int]]) -> int:
        ans = 0
        for col in zip(*grid):
            pre = -1
            for cur in col:
                if pre < cur:
                    pre = cur
                else:
                    pre += 1
                    ans += pre - cur
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int minimumOperations(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int ans = 0;
        for (int j = 0; j < n; ++j) {
            int pre = -1;
            for (int i = 0; i < m; ++i) {
                int cur = grid[i][j];
                if (pre < cur) {
                    pre = cur;
                } else {
                    ++pre;
                    ans += pre - cur;
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int minimumOperations(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int ans = 0;
        for (int j = 0; j < n; ++j) {
            int pre = -1;
            for (int i = 0; i < m; ++i) {
                int cur = grid[i][j];
                if (pre < cur) {
                    pre = cur;
                } else {
                    ++pre;
                    ans += pre - cur;
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
func minimumOperations(grid [][]int) (ans int) {
    m, n := len(grid), len(grid[0])
    for j := 0; j < n; j++ {
        pre := -1
        for i := 0; i < m; i++ {
            cur := grid[i][j]
            if pre < cur {
                pre = cur
            } else {
                pre++
                ans += pre - cur
            }
        }
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
function minimumOperations(grid: number[][]): number {
    const [m, n] = [grid.length, grid[0].length];
    let ans: number = 0;
    for (let j = 0; j < n; ++j) {
        let pre: number = -1;
        for (let i = 0; i < m; ++i) {
            const cur = grid[i][j];
            if (pre < cur) {
                pre = cur;
            } else {
                ++pre;
                ans += pre - cur;
            }
        }
    }
    return ans;
}

评论