二叉搜索树
二叉树
动态规划
树
深度优先搜索
题目描述
给定一个二叉树,找到其中最大的二叉搜索树(BST)子树,并返回该子树 的大小。其中,最大指的是子树节点数最多的。
二叉搜索树(BST) 中的所有节点都具备以下属性:
左子树的值小于其父(根)节点的值。
右子树的值大于其父(根)节点的值。
注意: 子树必须包含其所有后代。
示例 1:
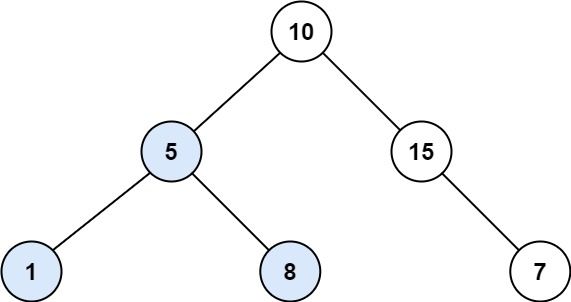
输入: root = [10,5,15,1,8,null,7]
输出: 3
解释: 本例中最大的 BST 子树是高亮显示的子树。返回值是子树的大小,即 3 。
示例 2:
输入: root = [4,2,7,2,3,5,null,2,null,null,null,null,null,1]
输出: 2
提示:
树上节点数目的范围是 [0, 104 ]
-104 <= Node.val <= 104
进阶: 你能想出 O(n) 时间复杂度的解法吗?
解法
方法一
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def largestBSTSubtree ( self , root : Optional [ TreeNode ]) -> int :
def dfs ( root ):
if root is None :
return inf , - inf , 0
lmi , lmx , ln = dfs ( root . left )
rmi , rmx , rn = dfs ( root . right )
nonlocal ans
if lmx < root . val < rmi :
ans = max ( ans , ln + rn + 1 )
return min ( lmi , root . val ), max ( rmx , root . val ), ln + rn + 1
return - inf , inf , 0
ans = 0
dfs ( root )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans ;
public int largestBSTSubtree ( TreeNode root ) {
ans = 0 ;
dfs ( root );
return ans ;
}
private int [] dfs ( TreeNode root ) {
if ( root == null ) {
return new int [] { Integer . MAX_VALUE , Integer . MIN_VALUE , 0 };
}
int [] left = dfs ( root . left );
int [] right = dfs ( root . right );
if ( left [ 1 ] < root . val && root . val < right [ 0 ] ) {
ans = Math . max ( ans , left [ 2 ] + right [ 2 ] + 1 );
return new int [] {
Math . min ( root . val , left [ 0 ] ), Math . max ( root . val , right [ 1 ] ), left [ 2 ] + right [ 2 ] + 1 };
}
return new int [] { Integer . MIN_VALUE , Integer . MAX_VALUE , 0 };
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
int ans ;
int largestBSTSubtree ( TreeNode * root ) {
ans = 0 ;
dfs ( root );
return ans ;
}
vector < int > dfs ( TreeNode * root ) {
if ( ! root ) return { INT_MAX , INT_MIN , 0 };
auto left = dfs ( root -> left );
auto right = dfs ( root -> right );
if ( left [ 1 ] < root -> val && root -> val < right [ 0 ]) {
ans = max ( ans , left [ 2 ] + right [ 2 ] + 1 );
return { min ( root -> val , left [ 0 ]), max ( root -> val , right [ 1 ]), left [ 2 ] + right [ 2 ] + 1 };
}
return { INT_MIN , INT_MAX , 0 };
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func largestBSTSubtree ( root * TreeNode ) int {
ans := 0
var dfs func ( root * TreeNode ) [] int
dfs = func ( root * TreeNode ) [] int {
if root == nil {
return [] int { math . MaxInt32 , math . MinInt32 , 0 }
}
left := dfs ( root . Left )
right := dfs ( root . Right )
if left [ 1 ] < root . Val && root . Val < right [ 0 ] {
ans = max ( ans , left [ 2 ] + right [ 2 ] + 1 )
return [] int { min ( root . Val , left [ 0 ]), max ( root . Val , right [ 1 ]), left [ 2 ] + right [ 2 ] + 1 }
}
return [] int { math . MinInt32 , math . MaxInt32 , 0 }
}
dfs ( root )
return ans
}
GitHub