


题目描述
给你一个整数 n 和一个二维整数数组 queries。
有 n 个城市,编号从 0 到 n - 1。初始时,每个城市 i 都有一条单向道路通往城市 i + 1( 0 <= i < n - 1)。
queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后,你需要找到从城市 0 到城市 n - 1 的最短路径的长度。
返回一个数组 answer,对于范围 [0, queries.length - 1] 中的每个 i,answer[i] 是处理完前 i + 1 个查询后,从城市 0 到城市 n - 1 的最短路径的长度。
示例 1:
输入: n = 5, queries = [[2, 4], [0, 2], [0, 4]]
输出: [3, 2, 1]
解释:

新增一条从 2 到 4 的道路后,从 0 到 4 的最短路径长度为 3。

新增一条从 0 到 2 的道路后,从 0 到 4 的最短路径长度为 2。
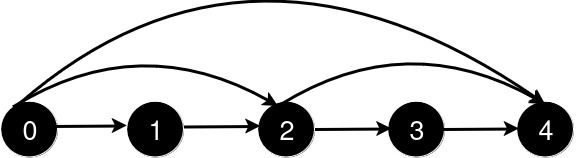
新增一条从 0 到 4 的道路后,从 0 到 4 的最短路径长度为 1。
示例 2:
输入: n = 4, queries = [[0, 3], [0, 2]]
输出: [1, 1]
解释:
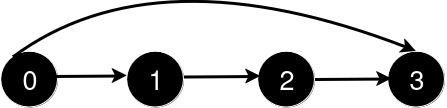
新增一条从 0 到 3 的道路后,从 0 到 3 的最短路径长度为 1。
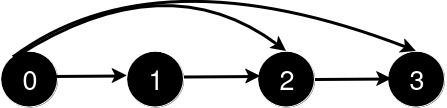
新增一条从 0 到 2 的道路后,从 0 到 3 的最短路径长度仍为 1。
提示:
3 <= n <= 5001 <= queries.length <= 500queries[i].length == 20 <= queries[i][0] < queries[i][1] < n1 < queries[i][1] - queries[i][0]- 查询中没有重复的道路。
解法
方法一:BFS
我们先建立一个有向图 \(\textit{g}\),其中 \(\textit{g}[i]\) 表示从城市 \(i\) 出发可以到达的城市列表,初始时,每个城市 \(i\) 都有一条单向道路通往城市 \(i + 1\)。
然后,我们对每个查询 \([u, v]\),将 \(v\) 添加到 \(u\) 的可达城市列表中,然后使用 BFS 求出从城市 \(0\) 到城市 \(n - 1\) 的最短路径长度,将结果添加到答案数组中。
最后返回答案数组即可。
时间复杂度 \(O(q \times (n + q))\),空间复杂度 \(O(n + q)\)。其中 \(n\) 和 \(q\) 分别为城市数量和查询数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | class Solution:
def shortestDistanceAfterQueries(
self, n: int, queries: List[List[int]]
) -> List[int]:
def bfs(i: int) -> int:
q = deque([i])
vis = [False] * n
vis[i] = True
d = 0
while 1:
for _ in range(len(q)):
u = q.popleft()
if u == n - 1:
return d
for v in g[u]:
if not vis[v]:
vis[v] = True
q.append(v)
d += 1
g = [[i + 1] for i in range(n - 1)]
ans = []
for u, v in queries:
g[u].append(v)
ans.append(bfs(0))
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 | class Solution {
private List<Integer>[] g;
private int n;
public int[] shortestDistanceAfterQueries(int n, int[][] queries) {
this.n = n;
g = new List[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (int i = 0; i < n - 1; ++i) {
g[i].add(i + 1);
}
int m = queries.length;
int[] ans = new int[m];
for (int i = 0; i < m; ++i) {
int u = queries[i][0], v = queries[i][1];
g[u].add(v);
ans[i] = bfs(0);
}
return ans;
}
private int bfs(int i) {
Deque<Integer> q = new ArrayDeque<>();
q.offer(i);
boolean[] vis = new boolean[n];
vis[i] = true;
for (int d = 0;; ++d) {
for (int k = q.size(); k > 0; --k) {
int u = q.poll();
if (u == n - 1) {
return d;
}
for (int v : g[u]) {
if (!vis[v]) {
vis[v] = true;
q.offer(v);
}
}
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | class Solution {
public:
vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
vector<int> g[n];
for (int i = 0; i < n - 1; ++i) {
g[i].push_back(i + 1);
}
auto bfs = [&](int i) -> int {
queue<int> q{{i}};
vector<bool> vis(n);
vis[i] = true;
for (int d = 0;; ++d) {
for (int k = q.size(); k; --k) {
int u = q.front();
q.pop();
if (u == n - 1) {
return d;
}
for (int v : g[u]) {
if (!vis[v]) {
vis[v] = true;
q.push(v);
}
}
}
}
};
vector<int> ans;
for (const auto& q : queries) {
g[q[0]].push_back(q[1]);
ans.push_back(bfs(0));
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 | func shortestDistanceAfterQueries(n int, queries [][]int) []int {
g := make([][]int, n)
for i := range g {
g[i] = append(g[i], i+1)
}
bfs := func(i int) int {
q := []int{i}
vis := make([]bool, n)
vis[i] = true
for d := 0; ; d++ {
for k := len(q); k > 0; k-- {
u := q[0]
if u == n-1 {
return d
}
q = q[1:]
for _, v := range g[u] {
if !vis[v] {
vis[v] = true
q = append(q, v)
}
}
}
}
}
ans := make([]int, len(queries))
for i, q := range queries {
g[q[0]] = append(g[q[0]], q[1])
ans[i] = bfs(0)
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 | function shortestDistanceAfterQueries(n: number, queries: number[][]): number[] {
const g: number[][] = Array.from({ length: n }, () => []);
for (let i = 0; i < n - 1; ++i) {
g[i].push(i + 1);
}
const bfs = (i: number): number => {
const q: number[] = [i];
const vis: boolean[] = Array(n).fill(false);
vis[i] = true;
for (let d = 0; ; ++d) {
const nq: number[] = [];
for (const u of q) {
if (u === n - 1) {
return d;
}
for (const v of g[u]) {
if (!vis[v]) {
vis[v] = true;
nq.push(v);
}
}
}
q.splice(0, q.length, ...nq);
}
};
const ans: number[] = [];
for (const [u, v] of queries) {
g[u].push(v);
ans.push(bfs(0));
}
return ans;
}
|







