


题目描述
给你一个 m x n 的二进制矩阵 grid 。
如果矩阵中一行或者一列从前往后与从后往前读是一样的,那么我们称这一行或者这一列是 回文 的。
你可以将 grid 中任意格子的值 翻转 ,也就是将格子里的值从 0 变成 1 ,或者从 1 变成 0 。
请你返回 最少 翻转次数,使得矩阵中 所有 行和列都是 回文的 ,且矩阵中 1 的数目可以被 4 整除 。
示例 1:
输入:grid = [[1,0,0],[0,1,0],[0,0,1]]
输出:3
解释:

示例 2:
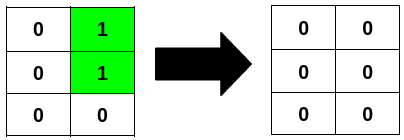
输入:grid = [[0,1],[0,1],[0,0]]
输出:2
解释:
示例 3:
输入:grid = [[1],[1]]
输出:2
解释:

提示:
m == grid.lengthn == grid[i].length1 <= m * n <= 2 * 1050 <= grid[i][j] <= 1
解法
方法一:分类讨论
行和列都是回文的,那么对于任意 \(i \in [0, m / 2)\) 和 \(j \in [0, n / 2)\),都需要满足 \(\text{grid}[i][j] = \text{grid}[m - i - 1][j] = \text{grid}[i][n - j - 1] = \text{grid}[m - i - 1][n - j - 1]\),要么都变成 \(0\),要么都变成 \(1\),变成 \(0\) 的次数为 \(c_0 = \text{grid}[i][j] + \text{grid}[m - i - 1][j] + \text{grid}[i][n - j - 1] + \text{grid}[m - i - 1][n - j - 1]\),变成 \(1\) 的次数为 \(c_1 = 4 - c_0\),取两者的较小值,累加到答案中。
接下来,我们再讨论 \(m\) 和 \(n\) 的奇偶性:
- 如果 \(m\) 和 \(n\) 都是偶数,那么直接返回答案;
- 如果 \(m\) 和 \(n\) 都是奇数,那么最中间的格子只能是 \(0\),因为题目要求 \(1\) 的数目可以被 \(4\) 整除;
- 如果 \(m\) 是奇数,而 \(n\) 是偶数,那么我们需要考虑最中间的一行;
- 如果 \(m\) 是偶数,而 \(n\) 是奇数,那么我们需要考虑最中间的一列。
对于后两种情况,我们需要统计最中间的一行或一列中对应位置不相同的格子对数 \(\text{diff}\),以及对应位置相同且为 \(1\) 的格子个数 \(\text{cnt1}\),然后再分情况讨论:
- 如果 \(\text{cnt1} \bmod 4 = 0\),那么我们只需要将 \(\text{diff}\) 个格子变成 \(0\) 即可,操作次数为 \(\text{diff}\);
- 否则,说明 \(\text{cnt1} = 2\),此时如果 \(\text{diff} \gt 0\),我们可以将其中一个格子变成 \(1\),使得 \(\text{cnt1} = 4\),那么剩下的 \(\text{diff} - 1\) 个格子变成 \(0\) 即可,操作次数一共为 \(\text{diff}\)。
- 否则,如果 \(\text{diff} = 0\),我们就把 \(\text{2}\) 个格子变成 \(0\),使得 \(\text{cnt1} \bmod 4 = 0\),操作次数为 \(\text{2}\)。
我们将操作次数累加到答案中,最后返回答案即可。
时间复杂度 \(O(m \times n)\),其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。空间复杂度 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | class Solution:
def minFlips(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
ans = 0
for i in range(m // 2):
for j in range(n // 2):
x, y = m - i - 1, n - j - 1
cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y]
ans += min(cnt1, 4 - cnt1)
if m % 2 and n % 2:
ans += grid[m // 2][n // 2]
diff = cnt1 = 0
if m % 2:
for j in range(n // 2):
if grid[m // 2][j] == grid[m // 2][n - j - 1]:
cnt1 += grid[m // 2][j] * 2
else:
diff += 1
if n % 2:
for i in range(m // 2):
if grid[i][n // 2] == grid[m - i - 1][n // 2]:
cnt1 += grid[i][n // 2] * 2
else:
diff += 1
ans += diff if cnt1 % 4 == 0 or diff else 2
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | class Solution {
public int minFlips(int[][] grid) {
int m = grid.length, n = grid[0].length;
int ans = 0;
for (int i = 0; i < m / 2; ++i) {
for (int j = 0; j < n / 2; ++j) {
int x = m - i - 1, y = n - j - 1;
int cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y];
ans += Math.min(cnt1, 4 - cnt1);
}
}
if (m % 2 == 1 && n % 2 == 1) {
ans += grid[m / 2][n / 2];
}
int diff = 0, cnt1 = 0;
if (m % 2 == 1) {
for (int j = 0; j < n / 2; ++j) {
if (grid[m / 2][j] == grid[m / 2][n - j - 1]) {
cnt1 += grid[m / 2][j] * 2;
} else {
diff += 1;
}
}
}
if (n % 2 == 1) {
for (int i = 0; i < m / 2; ++i) {
if (grid[i][n / 2] == grid[m - i - 1][n / 2]) {
cnt1 += grid[i][n / 2] * 2;
} else {
diff += 1;
}
}
}
ans += cnt1 % 4 == 0 || diff > 0 ? diff : 2;
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 | class Solution {
public:
int minFlips(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int ans = 0;
for (int i = 0; i < m / 2; ++i) {
for (int j = 0; j < n / 2; ++j) {
int x = m - i - 1, y = n - j - 1;
int cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y];
ans += min(cnt1, 4 - cnt1);
}
}
if (m % 2 == 1 && n % 2 == 1) {
ans += grid[m / 2][n / 2];
}
int diff = 0, cnt1 = 0;
if (m % 2 == 1) {
for (int j = 0; j < n / 2; ++j) {
if (grid[m / 2][j] == grid[m / 2][n - j - 1]) {
cnt1 += grid[m / 2][j] * 2;
} else {
diff += 1;
}
}
}
if (n % 2 == 1) {
for (int i = 0; i < m / 2; ++i) {
if (grid[i][n / 2] == grid[m - i - 1][n / 2]) {
cnt1 += grid[i][n / 2] * 2;
} else {
diff += 1;
}
}
}
ans += cnt1 % 4 == 0 || diff > 0 ? diff : 2;
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 | func minFlips(grid [][]int) int {
m, n := len(grid), len(grid[0])
ans := 0
for i := 0; i < m/2; i++ {
for j := 0; j < n/2; j++ {
x, y := m-i-1, n-j-1
cnt1 := grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y]
ans += min(cnt1, 4-cnt1)
}
}
if m%2 == 1 && n%2 == 1 {
ans += grid[m/2][n/2]
}
diff, cnt1 := 0, 0
if m%2 == 1 {
for j := 0; j < n/2; j++ {
if grid[m/2][j] == grid[m/2][n-j-1] {
cnt1 += grid[m/2][j] * 2
} else {
diff += 1
}
}
}
if n%2 == 1 {
for i := 0; i < m/2; i++ {
if grid[i][n/2] == grid[m-i-1][n/2] {
cnt1 += grid[i][n/2] * 2
} else {
diff += 1
}
}
}
if cnt1%4 == 0 || diff > 0 {
ans += diff
} else {
ans += 2
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44 | function minFlips(grid: number[][]): number {
const m = grid.length;
const n = grid[0].length;
let ans = 0;
for (let i = 0; i < Math.floor(m / 2); i++) {
for (let j = 0; j < Math.floor(n / 2); j++) {
const x = m - i - 1;
const y = n - j - 1;
const cnt1 = grid[i][j] + grid[x][j] + grid[i][y] + grid[x][y];
ans += Math.min(cnt1, 4 - cnt1);
}
}
if (m % 2 === 1 && n % 2 === 1) {
ans += grid[Math.floor(m / 2)][Math.floor(n / 2)];
}
let diff = 0,
cnt1 = 0;
if (m % 2 === 1) {
for (let j = 0; j < Math.floor(n / 2); j++) {
if (grid[Math.floor(m / 2)][j] === grid[Math.floor(m / 2)][n - j - 1]) {
cnt1 += grid[Math.floor(m / 2)][j] * 2;
} else {
diff += 1;
}
}
}
if (n % 2 === 1) {
for (let i = 0; i < Math.floor(m / 2); i++) {
if (grid[i][Math.floor(n / 2)] === grid[m - i - 1][Math.floor(n / 2)]) {
cnt1 += grid[i][Math.floor(n / 2)] * 2;
} else {
diff += 1;
}
}
}
ans += cnt1 % 4 === 0 || diff > 0 ? diff : 2;
return ans;
}
|





