


题目描述
给你两个正整数 xCorner 和 yCorner 和一个二维整数数组 circles ,其中 circles[i] = [xi, yi, ri] 表示一个圆心在 (xi, yi) 半径为 ri 的圆。
坐标平面内有一个左下角在原点,右上角在 (xCorner, yCorner) 的矩形。你需要判断是否存在一条从左下角到右上角的路径满足:路径 完全 在矩形内部,不会 触碰或者经过 任何 圆的内部和边界,同时 只 在起点和终点接触到矩形。
如果存在这样的路径,请你返回 true ,否则返回 false 。
示例 1:
输入:X = 3, Y = 4, circles = [[2,1,1]]
输出:true
解释:
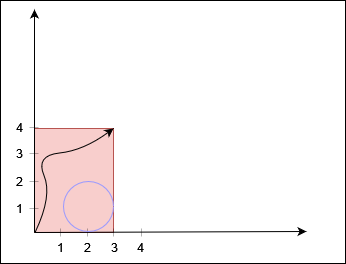
黑色曲线表示一条从 (0, 0) 到 (3, 4) 的路径。
示例 2:
输入:X = 3, Y = 3, circles = [[1,1,2]]
输出:false
解释:
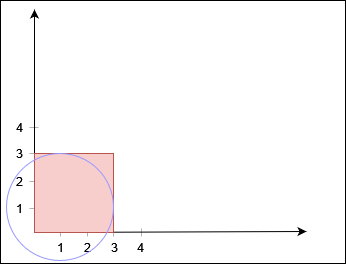
不存在从 (0, 0) 到 (3, 3) 的路径。
示例 3:
输入:X = 3, Y = 3, circles = [[2,1,1],[1,2,1]]
输出:false
解释:
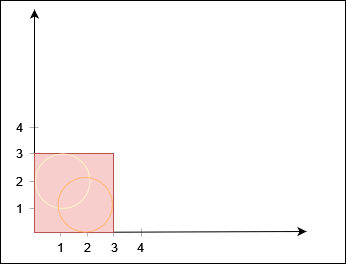
不存在从 (0, 0) 到 (3, 3) 的路径。
示例 4:
输入:X = 4, Y = 4, circles = [[5,5,1]]
输出:true
解释:
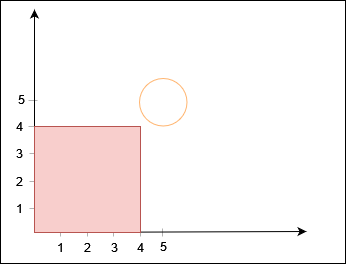
提示:
3 <= xCorner, yCorner <= 1091 <= circles.length <= 1000circles[i].length == 31 <= xi, yi, ri <= 109
解法
方法一:DFS + 数学
根据题意,我们分情况讨论:
当 circles 中只有一个圆时:
- 如果起点 \((0, 0)\) 在圆内(包括边界),或者终点 \((\textit{xCorner}, \textit{yCorner})\) 在圆内,那么无法满足“不触碰圆”的条件;
- 如果圆与矩形的左侧或上侧有交点,且与矩形的右侧或下侧有交点,这种情况下,圆会阻断从矩形左下角到右上角的路径,也无法满足“不触碰圆”的条件。
当 circles 中有多个圆时:
- 与上述情况类似,如果起点或终点在圆内时,无法满足“不触碰圆”的条件。
- 如果有多个圆,多个圆之间可能在矩形内相交,合并形成更大的障碍区域。只要这个障碍区域与矩形的左侧或上侧有交点,且与矩形的右侧或下侧有交点,那么无法满足“不触碰圆”的条件。如果相交区域不在矩形内部,不能进行合并,因为相交的区域无法阻断矩形内部路径。另外,如果相交的区域有一部分在矩形内,有一部分在矩形外,这些圆都可以作为搜索的起点或终点,可以合并,也可以不合并。我们只要任选相交的其中一个点,如果这个点在矩形内,我们就可以将这些圆合并。
根据上述分析,我们遍历所有圆,对于当前遍历到的圆,如果起点或终点在圆内,我们直接返回 false。否则,如果这个点没有被访问过,且这个圆与矩形的左侧或上侧有交点,我们就从这个圆开始进行深度优先搜索,搜索过程中,如果找到了一个圆,它与矩形的右侧或下侧有交点,说明圆形成的障碍区域阻断了从矩形左下角到右上角的路径,我们就返回 false。
我们定义 \(\textit{dfs}(i)\) 表示从第 \(i\) 个圆开始进行深度优先搜索,如果找到了一个圆,它与矩形的右侧或下侧有交点,返回 true,否则返回 false。
函数 \(\textit{dfs}(i)\) 的执行过程如下:
- 如果当前圆与矩形的右侧或下侧有交点,返回
true;
- 否则,我们将当前圆标记为已访问;
- 接下来,遍历其它所有圆,如果圆 \(j\) 没被访问过,且圆 \(i\) 和圆 \(j\) 相交,且这两个圆的其中一个交点在矩形内,我们就继续从圆 \(j\) 开始进行深度优先搜索,如果找到了一个圆,它与矩形的右侧或下侧有交点,返回
true;
- 如果没有找到这样的圆,返回
false。
上面的过程中,我们需要在圆 \(O_1 = (x_1, y_1, r_1)\) 和 \(O_2 = (x_2, y_2, r_2)\) 之间判断是否相交,如果两个圆相交,那么它们的圆心之间的距离不超过两个圆的半径之和,即 \((x_1 - x_2)^2 + (y_1 - y_2)^2 \le (r_1 + r_2)^2\)。
我们还需要寻找两个圆的一个交点,我们取一个点 \(A = (x, y)\),满足 \(\frac{O_1 A}{O_1 O_2} = \frac{r_1}{r_1 + r_2}\),如果两圆相交,那么点 \(A\) 一定在交集中,此时 \(\frac{x - x_1}{x_2 - x_1} = \frac{r_1}{r_1 + r_2}\),解得 \(x = \frac{x_1 r_2 + x_2 r_1}{r_1 + r_2}\),同理,有 \(y = \frac{y_1 r_2 + y_2 r_1}{r_1 + r_2}\)。只要这个点在矩形内,我们就可以继续进行深度优先搜索,即满足:
\[
\begin{cases}
x_1 r_2 + x_2 r_1 < (r_1 + r_2) \times \textit{xCorner} \\
y_1 r_2 + y_2 r_1 < (r_1 + r_2) \times \textit{yCorner}
\end{cases}
\]
时间复杂度 \(O(n^2)\),空间复杂度 \(O(n)\)。其中 \(n\) 为圆的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | class Solution:
def canReachCorner(
self, xCorner: int, yCorner: int, circles: List[List[int]]
) -> bool:
def in_circle(x: int, y: int, cx: int, cy: int, r: int) -> int:
return (x - cx) ** 2 + (y - cy) ** 2 <= r**2
def cross_left_top(cx: int, cy: int, r: int) -> bool:
a = abs(cx) <= r and 0 <= cy <= yCorner
b = abs(cy - yCorner) <= r and 0 <= cx <= xCorner
return a or b
def cross_right_bottom(cx: int, cy: int, r: int) -> bool:
a = abs(cx - xCorner) <= r and 0 <= cy <= yCorner
b = abs(cy) <= r and 0 <= cx <= xCorner
return a or b
def dfs(i: int) -> bool:
x1, y1, r1 = circles[i]
if cross_right_bottom(x1, y1, r1):
return True
vis[i] = True
for j, (x2, y2, r2) in enumerate(circles):
if vis[j] or not ((x1 - x2) ** 2 + (y1 - y2) ** 2 <= (r1 + r2) ** 2):
continue
if (
(x1 * r2 + x2 * r1 < (r1 + r2) * xCorner)
and (y1 * r2 + y2 * r1 < (r1 + r2) * yCorner)
and dfs(j)
):
return True
return False
vis = [False] * len(circles)
for i, (x, y, r) in enumerate(circles):
if in_circle(0, 0, x, y, r) or in_circle(xCorner, yCorner, x, y, r):
return False
if (not vis[i]) and cross_left_top(x, y, r) and dfs(i):
return False
return True
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64 | class Solution {
private int[][] circles;
private int xCorner, yCorner;
private boolean[] vis;
public boolean canReachCorner(int xCorner, int yCorner, int[][] circles) {
int n = circles.length;
this.circles = circles;
this.xCorner = xCorner;
this.yCorner = yCorner;
vis = new boolean[n];
for (int i = 0; i < n; ++i) {
var c = circles[i];
int x = c[0], y = c[1], r = c[2];
if (inCircle(0, 0, x, y, r) || inCircle(xCorner, yCorner, x, y, r)) {
return false;
}
if (!vis[i] && crossLeftTop(x, y, r) && dfs(i)) {
return false;
}
}
return true;
}
private boolean inCircle(long x, long y, long cx, long cy, long r) {
return (x - cx) * (x - cx) + (y - cy) * (y - cy) <= r * r;
}
private boolean crossLeftTop(long cx, long cy, long r) {
boolean a = Math.abs(cx) <= r && (cy >= 0 && cy <= yCorner);
boolean b = Math.abs(cy - yCorner) <= r && (cx >= 0 && cx <= xCorner);
return a || b;
}
private boolean crossRightBottom(long cx, long cy, long r) {
boolean a = Math.abs(cx - xCorner) <= r && (cy >= 0 && cy <= yCorner);
boolean b = Math.abs(cy) <= r && (cx >= 0 && cx <= xCorner);
return a || b;
}
private boolean dfs(int i) {
var c = circles[i];
long x1 = c[0], y1 = c[1], r1 = c[2];
if (crossRightBottom(x1, y1, r1)) {
return true;
}
vis[i] = true;
for (int j = 0; j < circles.length; ++j) {
var c2 = circles[j];
long x2 = c2[0], y2 = c2[1], r2 = c2[2];
if (vis[j]) {
continue;
}
if ((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) > (r1 + r2) * (r1 + r2)) {
continue;
}
if (x1 * r2 + x2 * r1 < (r1 + r2) * xCorner && y1 * r2 + y2 * r1 < (r1 + r2) * yCorner
&& dfs(j)) {
return true;
}
}
return false;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57 | class Solution {
public:
bool canReachCorner(int xCorner, int yCorner, vector<vector<int>>& circles) {
using ll = long long;
auto inCircle = [&](ll x, ll y, ll cx, ll cy, ll r) {
return (x - cx) * (x - cx) + (y - cy) * (y - cy) <= r * r;
};
auto crossLeftTop = [&](ll cx, ll cy, ll r) {
bool a = abs(cx) <= r && (cy >= 0 && cy <= yCorner);
bool b = abs(cy - yCorner) <= r && (cx >= 0 && cx <= xCorner);
return a || b;
};
auto crossRightBottom = [&](ll cx, ll cy, ll r) {
bool a = abs(cx - xCorner) <= r && (cy >= 0 && cy <= yCorner);
bool b = abs(cy) <= r && (cx >= 0 && cx <= xCorner);
return a || b;
};
int n = circles.size();
vector<bool> vis(n);
auto dfs = [&](this auto&& dfs, int i) -> bool {
auto c = circles[i];
ll x1 = c[0], y1 = c[1], r1 = c[2];
if (crossRightBottom(x1, y1, r1)) {
return true;
}
vis[i] = true;
for (int j = 0; j < n; ++j) {
if (vis[j]) {
continue;
}
auto c2 = circles[j];
ll x2 = c2[0], y2 = c2[1], r2 = c2[2];
if ((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) > (r1 + r2) * (r1 + r2)) {
continue;
}
if (x1 * r2 + x2 * r1 < (r1 + r2) * xCorner && y1 * r2 + y2 * r1 < (r1 + r2) * yCorner
&& dfs(j)) {
return true;
}
}
return false;
};
for (int i = 0; i < n; ++i) {
auto c = circles[i];
ll x = c[0], y = c[1], r = c[2];
if (inCircle(0, 0, x, y, r) || inCircle(xCorner, yCorner, x, y, r)) {
return false;
}
if (!vis[i] && crossLeftTop(x, y, r) && dfs(i)) {
return false;
}
}
return true;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61 | func canReachCorner(xCorner int, yCorner int, circles [][]int) bool {
inCircle := func(x, y, cx, cy, r int) bool {
dx, dy := x-cx, y-cy
return dx*dx+dy*dy <= r*r
}
crossLeftTop := func(cx, cy, r int) bool {
a := abs(cx) <= r && cy >= 0 && cy <= yCorner
b := abs(cy-yCorner) <= r && cx >= 0 && cx <= xCorner
return a || b
}
crossRightBottom := func(cx, cy, r int) bool {
a := abs(cx-xCorner) <= r && cy >= 0 && cy <= yCorner
b := abs(cy) <= r && cx >= 0 && cx <= xCorner
return a || b
}
vis := make([]bool, len(circles))
var dfs func(int) bool
dfs = func(i int) bool {
c := circles[i]
x1, y1, r1 := c[0], c[1], c[2]
if crossRightBottom(x1, y1, r1) {
return true
}
vis[i] = true
for j, c2 := range circles {
if vis[j] {
continue
}
x2, y2, r2 := c2[0], c2[1], c2[2]
if (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2) > (r1+r2)*(r1+r2) {
continue
}
if x1*r2+x2*r1 < (r1+r2)*xCorner && y1*r2+y2*r1 < (r1+r2)*yCorner && dfs(j) {
return true
}
}
return false
}
for i, c := range circles {
x, y, r := c[0], c[1], c[2]
if inCircle(0, 0, x, y, r) || inCircle(xCorner, yCorner, x, y, r) {
return false
}
if !vis[i] && crossLeftTop(x, y, r) && dfs(i) {
return false
}
}
return true
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63 | function canReachCorner(xCorner: number, yCorner: number, circles: number[][]): boolean {
const inCircle = (x: bigint, y: bigint, cx: bigint, cy: bigint, r: bigint): boolean => {
const dx = x - cx;
const dy = y - cy;
return dx * dx + dy * dy <= r * r;
};
const crossLeftTop = (cx: bigint, cy: bigint, r: bigint): boolean => {
const a = BigInt(Math.abs(Number(cx))) <= r && cy >= 0n && cy <= BigInt(yCorner);
const b =
BigInt(Math.abs(Number(cy - BigInt(yCorner)))) <= r &&
cx >= 0n &&
cx <= BigInt(xCorner);
return a || b;
};
const crossRightBottom = (cx: bigint, cy: bigint, r: bigint): boolean => {
const a =
BigInt(Math.abs(Number(cx - BigInt(xCorner)))) <= r &&
cy >= 0n &&
cy <= BigInt(yCorner);
const b = BigInt(Math.abs(Number(cy))) <= r && cx >= 0n && cx <= BigInt(xCorner);
return a || b;
};
const n = circles.length;
const vis: boolean[] = new Array(n).fill(false);
const dfs = (i: number): boolean => {
const [x1, y1, r1] = circles[i].map(BigInt);
if (crossRightBottom(x1, y1, r1)) {
return true;
}
vis[i] = true;
for (let j = 0; j < n; j++) {
if (vis[j]) continue;
const [x2, y2, r2] = circles[j].map(BigInt);
if ((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) > (r1 + r2) * (r1 + r2)) {
continue;
}
if (
x1 * r2 + x2 * r1 < (r1 + r2) * BigInt(xCorner) &&
y1 * r2 + y2 * r1 < (r1 + r2) * BigInt(yCorner) &&
dfs(j)
) {
return true;
}
}
return false;
};
for (let i = 0; i < n; i++) {
const [x, y, r] = circles[i].map(BigInt);
if (inCircle(0n, 0n, x, y, r) || inCircle(BigInt(xCorner), BigInt(yCorner), x, y, r)) {
return false;
}
if (!vis[i] && crossLeftTop(x, y, r) && dfs(i)) {
return false;
}
}
return true;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85 | impl Solution {
pub fn can_reach_corner(x_corner: i32, y_corner: i32, circles: Vec<Vec<i32>>) -> bool {
let n = circles.len();
let mut vis = vec![false; n];
let in_circle = |x: i64, y: i64, cx: i64, cy: i64, r: i64| -> bool {
(x - cx) * (x - cx) + (y - cy) * (y - cy) <= r * r
};
let cross_left_top = |cx: i64, cy: i64, r: i64| -> bool {
let a = cx.abs() <= r && (cy >= 0 && cy <= y_corner as i64);
let b = (cy - y_corner as i64).abs() <= r && (cx >= 0 && cx <= x_corner as i64);
a || b
};
let cross_right_bottom = |cx: i64, cy: i64, r: i64| -> bool {
let a = (cx - x_corner as i64).abs() <= r && (cy >= 0 && cy <= y_corner as i64);
let b = cy.abs() <= r && (cx >= 0 && cx <= x_corner as i64);
a || b
};
fn dfs(
circles: &Vec<Vec<i32>>,
vis: &mut Vec<bool>,
i: usize,
x_corner: i32,
y_corner: i32,
cross_right_bottom: &dyn Fn(i64, i64, i64) -> bool,
) -> bool {
let c = &circles[i];
let (x1, y1, r1) = (c[0] as i64, c[1] as i64, c[2] as i64);
if cross_right_bottom(x1, y1, r1) {
return true;
}
vis[i] = true;
for j in 0..circles.len() {
if vis[j] {
continue;
}
let c2 = &circles[j];
let (x2, y2, r2) = (c2[0] as i64, c2[1] as i64, c2[2] as i64);
if (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) > (r1 + r2) * (r1 + r2) {
continue;
}
if x1 * r2 + x2 * r1 < (r1 + r2) * x_corner as i64
&& y1 * r2 + y2 * r1 < (r1 + r2) * y_corner as i64
&& dfs(circles, vis, j, x_corner, y_corner, cross_right_bottom)
{
return true;
}
}
false
}
for i in 0..n {
let c = &circles[i];
let (x, y, r) = (c[0] as i64, c[1] as i64, c[2] as i64);
if in_circle(0, 0, x, y, r) || in_circle(x_corner as i64, y_corner as i64, x, y, r) {
return false;
}
if !vis[i]
&& cross_left_top(x, y, r)
&& dfs(
&circles,
&mut vis,
i,
x_corner,
y_corner,
&cross_right_bottom,
)
{
return false;
}
}
true
}
}
|






