


题目描述
有一个 m x n 大小的矩形蛋糕,需要切成 1 x 1 的小块。
给你整数 m ,n 和两个数组:
horizontalCut 的大小为 m - 1 ,其中 horizontalCut[i] 表示沿着水平线 i 切蛋糕的开销。verticalCut 的大小为 n - 1 ,其中 verticalCut[j] 表示沿着垂直线 j 切蛋糕的开销。
一次操作中,你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一:
- 沿着水平线
i 切开蛋糕,开销为 horizontalCut[i] 。
- 沿着垂直线
j 切开蛋糕,开销为 verticalCut[j] 。
每次操作后,这块蛋糕都被切成两个独立的小蛋糕。
每次操作的开销都为最开始对应切割线的开销,并且不会改变。
请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。
示例 1:
输入:m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]
输出:13
解释:
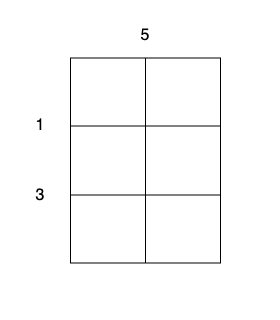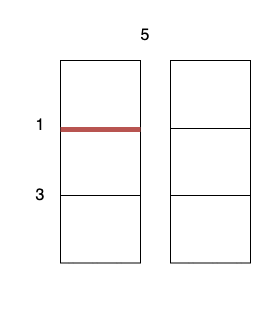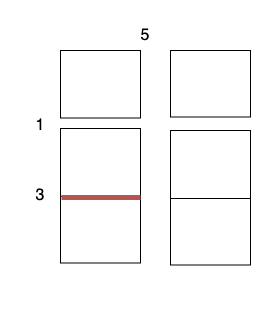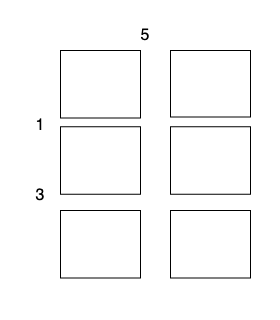
- 沿着垂直线 0 切开蛋糕,开销为 5 。
- 沿着水平线 0 切开
3 x 1 的蛋糕块,开销为 1 。
- 沿着水平线 0 切开
3 x 1 的蛋糕块,开销为 1 。
- 沿着水平线 1 切开
2 x 1 的蛋糕块,开销为 3 。
- 沿着水平线 1 切开
2 x 1 的蛋糕块,开销为 3 。
总开销为 5 + 1 + 1 + 3 + 3 = 13 。
示例 2:
输入:m = 2, n = 2, horizontalCut = [7], verticalCut = [4]
输出:15
解释:
- 沿着水平线 0 切开蛋糕,开销为 7 。
- 沿着垂直线 0 切开
1 x 2 的蛋糕块,开销为 4 。
- 沿着垂直线 0 切开
1 x 2 的蛋糕块,开销为 4 。
总开销为 7 + 4 + 4 = 15 。
提示:
1 <= m, n <= 105horizontalCut.length == m - 1verticalCut.length == n - 11 <= horizontalCut[i], verticalCut[i] <= 103
解法
方法一:贪心 + 双指针
对于一个位置,越早切,所需要切的次数越少,因此,显然是开销越大的位置越早切。
所以,我们可以对数组 \(\textit{horizontalCut}\) 和 \(\textit{verticalCut}\) 按照从大到小的顺序排序,然后使用两个指针 \(i\) 和 \(j\) 分别指向 \(\textit{horizontalCut}\) 和 \(\textit{verticalCut}\) 的开销,每次选择开销较大的位置进行切割,同时更新对应的行数和列数。
每次在水平方向上切割时,如果此前列数为 \(v\),那么此次的开销为 \(\textit{horizontalCut}[i] \times v\),然后行数 \(h\) 加一;同理,每次在垂直方向上切割时,如果此前行数为 \(h\),那么此次的开销为 \(\textit{verticalCut}[j] \times h\),然后列数 \(v\) 加一。
最后,当 \(i\) 和 \(j\) 都到达末尾时,返回总开销即可。
时间复杂度 \(O(m \times \log m + n \times \log n)\),空间复杂度 \(O(\log m + \log n)\)。其中 \(m\) 和 \(n\) 分别为 \(\textit{horizontalCut}\) 和 \(\textit{verticalCut}\) 的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | class Solution:
def minimumCost(
self, m: int, n: int, horizontalCut: List[int], verticalCut: List[int]
) -> int:
horizontalCut.sort(reverse=True)
verticalCut.sort(reverse=True)
ans = i = j = 0
h = v = 1
while i < m - 1 or j < n - 1:
if j == n - 1 or (i < m - 1 and horizontalCut[i] > verticalCut[j]):
ans += horizontalCut[i] * v
h, i = h + 1, i + 1
else:
ans += verticalCut[j] * h
v, j = v + 1, j + 1
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | class Solution {
public long minimumCost(int m, int n, int[] horizontalCut, int[] verticalCut) {
Arrays.sort(horizontalCut);
Arrays.sort(verticalCut);
long ans = 0;
int i = m - 2, j = n - 2;
int h = 1, v = 1;
while (i >= 0 || j >= 0) {
if (j < 0 || (i >= 0 && horizontalCut[i] > verticalCut[j])) {
ans += 1L * horizontalCut[i--] * v;
++h;
} else {
ans += 1L * verticalCut[j--] * h;
++v;
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution {
public:
long long minimumCost(int m, int n, vector<int>& horizontalCut, vector<int>& verticalCut) {
sort(horizontalCut.rbegin(), horizontalCut.rend());
sort(verticalCut.rbegin(), verticalCut.rend());
long long ans = 0;
int i = 0, j = 0;
int h = 1, v = 1;
while (i < m - 1 || j < n - 1) {
if (j == n - 1 || (i < m - 1 && horizontalCut[i] > verticalCut[j])) {
ans += 1LL * horizontalCut[i++] * v;
h++;
} else {
ans += 1LL * verticalCut[j++] * h;
v++;
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | func minimumCost(m int, n int, horizontalCut []int, verticalCut []int) (ans int64) {
sort.Sort(sort.Reverse(sort.IntSlice(horizontalCut)))
sort.Sort(sort.Reverse(sort.IntSlice(verticalCut)))
i, j := 0, 0
h, v := 1, 1
for i < m-1 || j < n-1 {
if j == n-1 || (i < m-1 && horizontalCut[i] > verticalCut[j]) {
ans += int64(horizontalCut[i] * v)
h++
i++
} else {
ans += int64(verticalCut[j] * h)
v++
j++
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | function minimumCost(m: number, n: number, horizontalCut: number[], verticalCut: number[]): number {
horizontalCut.sort((a, b) => b - a);
verticalCut.sort((a, b) => b - a);
let ans = 0;
let [i, j] = [0, 0];
let [h, v] = [1, 1];
while (i < m - 1 || j < n - 1) {
if (j === n - 1 || (i < m - 1 && horizontalCut[i] > verticalCut[j])) {
ans += horizontalCut[i] * v;
h++;
i++;
} else {
ans += verticalCut[j] * h;
v++;
j++;
}
}
return ans;
}
|



