跳转至

3197. 包含所有 1 的最小矩形面积 II

题目描述

给你一个二维 二进制 数组 grid。你需要找到 3 个 不重叠、面积 非零 、边在水平方向和竖直方向上的矩形，并且满足 grid 中所有的 1 都在这些矩形的内部。

返回这些矩形面积之和的 最小 可能值。

注意，这些矩形可以相接。

 

示例 1：

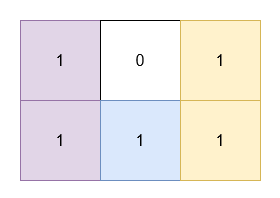
输入： grid = [[1,0,1],[1,1,1]]

输出： 5

解释：

  • 位于 (0, 0) 和 (1, 0) 的 1 被一个面积为 2 的矩形覆盖。
  • 位于 (0, 2) 和 (1, 2) 的 1 被一个面积为 2 的矩形覆盖。
  • 位于 (1, 1) 的 1 被一个面积为 1 的矩形覆盖。

示例 2：

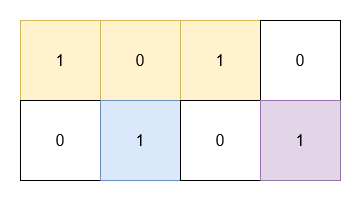
输入： grid = [[1,0,1,0],[0,1,0,1]]

输出： 5

解释：

  • 位于 (0, 0) 和 (0, 2) 的 1 被一个面积为 3 的矩形覆盖。
  • 位于 (1, 1) 的 1 被一个面积为 1 的矩形覆盖。
  • 位于 (1, 3) 的 1 被一个面积为 1 的矩形覆盖。

 

提示：

  • 1 <= grid.length, grid[i].length <= 30
  • grid[i][j] 是 0 或 1。
  • 输入保证 grid 中至少有三个 1 。

解法

方法一：枚举

根据题目描述，我们可以用两条分割线，将矩形分成三个部分，我们分别计算每一部分包含所有 $1$ 的最小矩形面积，然后取三个部分面积之和的最小值。

我们可以枚举两条分割线的位置，共有 $6$ 种情况：

  1. 两次横向分割
  2. 两次纵向分割
  3. 先进行一次横向分割，再对上部分进行一次纵向分割
  4. 先进行一次横向分割，再对下部分进行一次纵向分割
  5. 先进行一次纵向分割，再对左部分进行一次横向分割
  6. 先进行一次纵向分割，再对右部分进行一次横向分割

我们可以用一个函数 $\textit{f}(i_1, j_1, i_2, j_2)$ 来计算矩形 $(i_1, j_1)$ 到 $(i_2, j_2)$ 包含所有 $1$ 的最小矩形面积。

时间复杂度 $O(m^2 \times n^2)$，其中 $m$ 和 $n$ 分别是矩形的行数和列数。空间复杂度 $O(1)$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution:
    def minimumSum(self, grid: List[List[int]]) -> int:
        def f(i1: int, j1: int, i2: int, j2: int) -> int:
            x1 = y1 = inf
            x2 = y2 = -inf
            for i in range(i1, i2 + 1):
                for j in range(j1, j2 + 1):
                    if grid[i][j] == 1:
                        x1 = min(x1, i)
                        y1 = min(y1, j)
                        x2 = max(x2, i)
                        y2 = max(y2, j)
            return (x2 - x1 + 1) * (y2 - y1 + 1)

        m, n = len(grid), len(grid[0])
        ans = m * n
        for i1 in range(m - 1):
            for i2 in range(i1 + 1, m - 1):
                ans = min(
                    ans,
                    f(0, 0, i1, n - 1)
                    + f(i1 + 1, 0, i2, n - 1)
                    + f(i2 + 1, 0, m - 1, n - 1),
                )
        for j1 in range(n - 1):
            for j2 in range(j1 + 1, n - 1):
                ans = min(
                    ans,
                    f(0, 0, m - 1, j1)
                    + f(0, j1 + 1, m - 1, j2)
                    + f(0, j2 + 1, m - 1, n - 1),
                )
        for i in range(m - 1):
            for j in range(n - 1):
                ans = min(
                    ans,
                    f(0, 0, i, j) + f(0, j + 1, i, n - 1) + f(i + 1, 0, m - 1, n - 1),
                )
                ans = min(
                    ans,
                    f(0, 0, i, n - 1)
                    + f(i + 1, 0, m - 1, j)
                    + f(i + 1, j + 1, m - 1, n - 1),
                )

                ans = min(
                    ans,
                    f(0, 0, i, j) + f(i + 1, 0, m - 1, j) + f(0, j + 1, m - 1, n - 1),
                )
                ans = min(
                    ans,
                    f(0, 0, m - 1, j)
                    + f(0, j + 1, i, n - 1)
                    + f(i + 1, j + 1, m - 1, n - 1),
                )
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    private final int inf = 1 << 30;
    private int[][] grid;

    public int minimumSum(int[][] grid) {
        this.grid = grid;
        int m = grid.length;
        int n = grid[0].length;
        int ans = m * n;

        for (int i1 = 0; i1 < m - 1; i1++) {
            for (int i2 = i1 + 1; i2 < m - 1; i2++) {
                ans = Math.min(
                    ans, f(0, 0, i1, n - 1) + f(i1 + 1, 0, i2, n - 1) + f(i2 + 1, 0, m - 1, n - 1));
            }
        }

        for (int j1 = 0; j1 < n - 1; j1++) {
            for (int j2 = j1 + 1; j2 < n - 1; j2++) {
                ans = Math.min(
                    ans, f(0, 0, m - 1, j1) + f(0, j1 + 1, m - 1, j2) + f(0, j2 + 1, m - 1, n - 1));
            }
        }

        for (int i = 0; i < m - 1; i++) {
            for (int j = 0; j < n - 1; j++) {
                ans = Math.min(
                    ans, f(0, 0, i, j) + f(0, j + 1, i, n - 1) + f(i + 1, 0, m - 1, n - 1));
                ans = Math.min(
                    ans, f(0, 0, i, n - 1) + f(i + 1, 0, m - 1, j) + f(i + 1, j + 1, m - 1, n - 1));

                ans = Math.min(
                    ans, f(0, 0, i, j) + f(i + 1, 0, m - 1, j) + f(0, j + 1, m - 1, n - 1));
                ans = Math.min(
                    ans, f(0, 0, m - 1, j) + f(0, j + 1, i, n - 1) + f(i + 1, j + 1, m - 1, n - 1));
            }
        }
        return ans;
    }

    private int f(int i1, int j1, int i2, int j2) {
        int x1 = inf, y1 = inf;
        int x2 = -inf, y2 = -inf;
        for (int i = i1; i <= i2; i++) {
            for (int j = j1; j <= j2; j++) {
                if (grid[i][j] == 1) {
                    x1 = Math.min(x1, i);
                    y1 = Math.min(y1, j);
                    x2 = Math.max(x2, i);
                    y2 = Math.max(y2, j);
                }
            }
        }
        return (x2 - x1 + 1) * (y2 - y1 + 1);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    int minimumSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        int ans = m * n;
        int inf = INT_MAX / 4;
        auto f = [&](int i1, int j1, int i2, int j2) {
            int x1 = inf, y1 = inf;
            int x2 = -inf, y2 = -inf;
            for (int i = i1; i <= i2; i++) {
                for (int j = j1; j <= j2; j++) {
                    if (grid[i][j] == 1) {
                        x1 = min(x1, i);
                        y1 = min(y1, j);
                        x2 = max(x2, i);
                        y2 = max(y2, j);
                    }
                }
            }
            return x1 > x2 || y1 > y2 ? inf : (x2 - x1 + 1) * (y2 - y1 + 1);
        };

        for (int i1 = 0; i1 < m - 1; i1++) {
            for (int i2 = i1 + 1; i2 < m - 1; i2++) {
                ans = min(ans, f(0, 0, i1, n - 1) + f(i1 + 1, 0, i2, n - 1) + f(i2 + 1, 0, m - 1, n - 1));
            }
        }

        for (int j1 = 0; j1 < n - 1; j1++) {
            for (int j2 = j1 + 1; j2 < n - 1; j2++) {
                ans = min(ans, f(0, 0, m - 1, j1) + f(0, j1 + 1, m - 1, j2) + f(0, j2 + 1, m - 1, n - 1));
            }
        }

        for (int i = 0; i < m - 1; i++) {
            for (int j = 0; j < n - 1; j++) {
                ans = min(ans, f(0, 0, i, j) + f(0, j + 1, i, n - 1) + f(i + 1, 0, m - 1, n - 1));
                ans = min(ans, f(0, 0, i, n - 1) + f(i + 1, 0, m - 1, j) + f(i + 1, j + 1, m - 1, n - 1));
                ans = min(ans, f(0, 0, i, j) + f(i + 1, 0, m - 1, j) + f(0, j + 1, m - 1, n - 1));
                ans = min(ans, f(0, 0, m - 1, j) + f(0, j + 1, i, n - 1) + f(i + 1, j + 1, m - 1, n - 1));
            }
        }

        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
func minimumSum(grid [][]int) int {
    m := len(grid)
    n := len(grid[0])
    ans := m * n
    inf := math.MaxInt32

    f := func(i1, j1, i2, j2 int) int {
        x1, y1 := inf, inf
        x2, y2 := -inf, -inf
        for i := i1; i <= i2; i++ {
            for j := j1; j <= j2; j++ {
                if grid[i][j] == 1 {
                    x1 = min(x1, i)
                    y1 = min(y1, j)
                    x2 = max(x2, i)
                    y2 = max(y2, j)
                }
            }
        }
        if x1 == inf {
            return 0
        }
        return (x2 - x1 + 1) * (y2 - y1 + 1)
    }

    for i1 := 0; i1 < m-1; i1++ {
        for i2 := i1 + 1; i2 < m-1; i2++ {
            ans = min(ans, f(0, 0, i1, n-1)+f(i1+1, 0, i2, n-1)+f(i2+1, 0, m-1, n-1))
        }
    }

    for j1 := 0; j1 < n-1; j1++ {
        for j2 := j1 + 1; j2 < n-1; j2++ {
            ans = min(ans, f(0, 0, m-1, j1)+f(0, j1+1, m-1, j2)+f(0, j2+1, m-1, n-1))
        }
    }

    for i := 0; i < m-1; i++ {
        for j := 0; j < n-1; j++ {
            ans = min(ans, f(0, 0, i, j)+f(0, j+1, i, n-1)+f(i+1, 0, m-1, n-1))
            ans = min(ans, f(0, 0, i, n-1)+f(i+1, 0, m-1, j)+f(i+1, j+1, m-1, n-1))
            ans = min(ans, f(0, 0, i, j)+f(i+1, 0, m-1, j)+f(0, j+1, m-1, n-1))
            ans = min(ans, f(0, 0, m-1, j)+f(0, j+1, i, n-1)+f(i+1, j+1, m-1, n-1))
        }
    }

    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
function minimumSum(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    let ans = m * n;
    const inf = Number.MAX_SAFE_INTEGER;
    const f = (i1: number, j1: number, i2: number, j2: number): number => {
        let [x1, y1] = [inf, inf];
        let [x2, y2] = [-inf, -inf];
        for (let i = i1; i <= i2; i++) {
            for (let j = j1; j <= j2; j++) {
                if (grid[i][j] === 1) {
                    x1 = Math.min(x1, i);
                    y1 = Math.min(y1, j);
                    x2 = Math.max(x2, i);
                    y2 = Math.max(y2, j);
                }
            }
        }
        return x1 === inf ? 0 : (x2 - x1 + 1) * (y2 - y1 + 1);
    };

    for (let i1 = 0; i1 < m - 1; i1++) {
        for (let i2 = i1 + 1; i2 < m - 1; i2++) {
            ans = Math.min(
                ans,
                f(0, 0, i1, n - 1) + f(i1 + 1, 0, i2, n - 1) + f(i2 + 1, 0, m - 1, n - 1),
            );
        }
    }

    for (let j1 = 0; j1 < n - 1; j1++) {
        for (let j2 = j1 + 1; j2 < n - 1; j2++) {
            ans = Math.min(
                ans,
                f(0, 0, m - 1, j1) + f(0, j1 + 1, m - 1, j2) + f(0, j2 + 1, m - 1, n - 1),
            );
        }
    }

    for (let i = 0; i < m - 1; i++) {
        for (let j = 0; j < n - 1; j++) {
            ans = Math.min(ans, f(0, 0, i, j) + f(0, j + 1, i, n - 1) + f(i + 1, 0, m - 1, n - 1));
            ans = Math.min(
                ans,
                f(0, 0, i, n - 1) + f(i + 1, 0, m - 1, j) + f(i + 1, j + 1, m - 1, n - 1),
            );
            ans = Math.min(ans, f(0, 0, i, j) + f(i + 1, 0, m - 1, j) + f(0, j + 1, m - 1, n - 1));
            ans = Math.min(
                ans,
                f(0, 0, m - 1, j) + f(0, j + 1, i, n - 1) + f(i + 1, j + 1, m - 1, n - 1),
            );
        }
    }

    return ans;
}

评论