


题目描述
给你一个数组 nums ,它是 [0, 1, 2, ..., n - 1] 的一个排列 。对于任意一个 [0, 1, 2, ..., n - 1] 的排列 perm ,其 分数 定义为:
score(perm) = |perm[0] - nums[perm[1]]| + |perm[1] - nums[perm[2]]| + ... + |perm[n - 1] - nums[perm[0]]|
返回具有 最低 分数的排列 perm 。如果存在多个满足题意且分数相等的排列,则返回其中字典序最小的一个。
示例 1:
输入:nums = [1,0,2]
输出:[0,1,2]
解释:
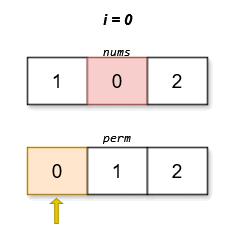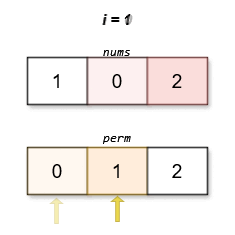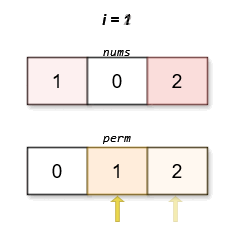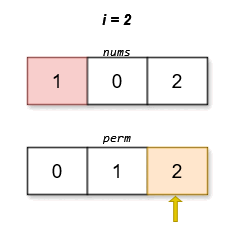
字典序最小且分数最低的排列是 [0,1,2]。这个排列的分数是 |0 - 0| + |1 - 2| + |2 - 1| = 2 。
示例 2:
输入:nums = [0,2,1]
输出:[0,2,1]
解释:
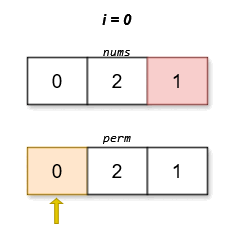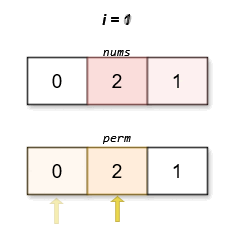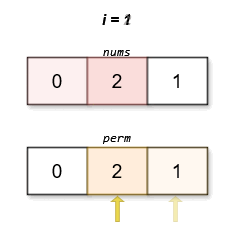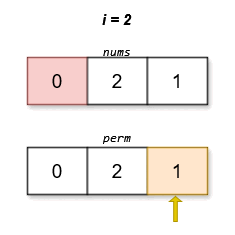
字典序最小且分数最低的排列是 [0,2,1]。这个排列的分数是 |0 - 1| + |2 - 2| + |1 - 0| = 2 。
提示:
2 <= n == nums.length <= 14nums 是 [0, 1, 2, ..., n - 1] 的一个排列。
解法
方法一:记忆化搜索
我们注意到,对于任意一个排列 \(\textit{perm}\),把它循环向左移动任意次,得到的排列分数依然是相同的。由于题目要求返回字典序最小的排列,因此我们可以确定排列的第一个元素一定是 \(0\)。
另外,由于题目的数据范围不超过 \(14\),我们可以考虑使用状态压缩的方法,来表示当前排列选取的数字集合。我们用一个长度为 \(n\) 的二进制数 \(\textit{mask}\) 来表示当前排列选取的数字集合,其中 \(\textit{mask}\) 的第 \(i\) 位为 \(1\) 表示数字 \(i\) 已经被选取,为 \(0\) 表示数字 \(i\) 还未被选取。
我们设计一个函数 \(\textit{dfs}(\textit{mask}, \textit{pre})\),表示当前排列选取的数字集合为 \(\textit{mask}\),且最后一个选取的数字为 \(\textit{pre}\) 时,得到的排列的最小分数。初始时我们将数字 \(0\) 加入到排列中。
函数 \(\textit{dfs}(\textit{mask}, \textit{pre})\) 的计算过程如下:
- 如果 \(\textit{mask}\) 的二进制表示中 \(1\) 的个数为 \(n\),即 \(\textit{mask} = 2^n - 1\),表示所有数字都已经被选取,此时返回 \(|\textit{pre} - \textit{nums}[0]|\);
- 否则,我们枚举下一个选取的数字 \(\textit{cur}\),如果数字 \(\textit{cur}\) 还未被选取,那么我们可以将数字 \(\textit{cur}\) 加入到排列中,此时排列的分数为 \(|\textit{pre} - \textit{nums}[\textit{cur}]| + \textit{dfs}(\textit{mask} \, | \, 1 << \textit{cur}, \textit{cur})\),我们需要取所有 \(\textit{cur}\) 中分数的最小值。
最后,我们利用一个函数 \(\textit{g}(\textit{mask}, \textit{pre})\) 来构造得到最小分数的排列。我们首先将数字 \(\textit{pre}\) 加入到排列中,然后枚举下一个选取的数字 \(\textit{cur}\),如果数字 \(\textit{cur}\) 还未被选取,且满足 \(|\textit{pre} - \textit{nums}[\textit{cur}]| + \textit{dfs}(\textit{mask} \, | \, 1 << \textit{cur}, \textit{cur})\) 的值等于 \(\textit{dfs}(\textit{mask}, \textit{pre})\),那么我们就可以将数字 \(\textit{cur}\) 加入到排列中。
时间复杂度 \((n^2 \times 2^n)\),空间复杂度 \(O(n \times 2^n)\)。其中 \(n\) 为数组 \(\textit{nums}\) 的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution:
def findPermutation(self, nums: List[int]) -> List[int]:
@cache
def dfs(mask: int, pre: int) -> int:
if mask == (1 << n) - 1:
return abs(pre - nums[0])
res = inf
for cur in range(1, n):
if mask >> cur & 1 ^ 1:
res = min(res, abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur))
return res
def g(mask: int, pre: int):
ans.append(pre)
if mask == (1 << n) - 1:
return
res = dfs(mask, pre)
for cur in range(1, n):
if mask >> cur & 1 ^ 1:
if abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur) == res:
g(mask | 1 << cur, cur)
break
n = len(nums)
ans = []
g(1, 0)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 | class Solution {
private Integer[][] f;
private int[] nums;
private int[] ans;
private int n;
public int[] findPermutation(int[] nums) {
n = nums.length;
ans = new int[n];
this.nums = nums;
f = new Integer[1 << n][n];
g(1, 0, 0);
return ans;
}
private int dfs(int mask, int pre) {
if (mask == (1 << n) - 1) {
return Math.abs(pre - nums[0]);
}
if (f[mask][pre] != null) {
return f[mask][pre];
}
int res = Integer.MAX_VALUE;
for (int cur = 1; cur < n; ++cur) {
if ((mask >> cur & 1) == 0) {
res = Math.min(res, Math.abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur));
}
}
return f[mask][pre] = res;
}
private void g(int mask, int pre, int k) {
ans[k] = pre;
if (mask == (1 << n) - 1) {
return;
}
int res = dfs(mask, pre);
for (int cur = 1; cur < n; ++cur) {
if ((mask >> cur & 1) == 0) {
if (Math.abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur) == res) {
g(mask | 1 << cur, cur, k + 1);
break;
}
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 | class Solution {
public:
vector<int> findPermutation(vector<int>& nums) {
int n = nums.size();
vector<int> ans;
int f[1 << n][n];
memset(f, -1, sizeof(f));
function<int(int, int)> dfs = [&](int mask, int pre) {
if (mask == (1 << n) - 1) {
return abs(pre - nums[0]);
}
int* res = &f[mask][pre];
if (*res != -1) {
return *res;
}
*res = INT_MAX;
for (int cur = 1; cur < n; ++cur) {
if (mask >> cur & 1 ^ 1) {
*res = min(*res, abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur));
}
}
return *res;
};
function<void(int, int)> g = [&](int mask, int pre) {
ans.push_back(pre);
if (mask == (1 << n) - 1) {
return;
}
int res = dfs(mask, pre);
for (int cur = 1; cur < n; ++cur) {
if (mask >> cur & 1 ^ 1) {
if (abs(pre - nums[cur]) + dfs(mask | 1 << cur, cur) == res) {
g(mask | 1 << cur, cur);
break;
}
}
}
};
g(1, 0);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52 | func findPermutation(nums []int) (ans []int) {
n := len(nums)
f := make([][]int, 1<<n)
for i := range f {
f[i] = make([]int, n)
for j := range f[i] {
f[i][j] = -1
}
}
var dfs func(int, int) int
dfs = func(mask, pre int) int {
if mask == 1<<n-1 {
return abs(pre - nums[0])
}
if f[mask][pre] != -1 {
return f[mask][pre]
}
res := &f[mask][pre]
*res = math.MaxInt32
for cur := 1; cur < n; cur++ {
if mask>>cur&1 == 0 {
*res = min(*res, abs(pre-nums[cur])+dfs(mask|1<<cur, cur))
}
}
return *res
}
var g func(int, int)
g = func(mask, pre int) {
ans = append(ans, pre)
if mask == 1<<n-1 {
return
}
res := dfs(mask, pre)
for cur := 1; cur < n; cur++ {
if mask>>cur&1 == 0 {
if abs(pre-nums[cur])+dfs(mask|1<<cur, cur) == res {
g(mask|1<<cur, cur)
break
}
}
}
}
g(1, 0)
return
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 | function findPermutation(nums: number[]): number[] {
const n = nums.length;
const ans: number[] = [];
const f: number[][] = Array.from({ length: 1 << n }, () => Array(n).fill(-1));
const dfs = (mask: number, pre: number): number => {
if (mask === (1 << n) - 1) {
return Math.abs(pre - nums[0]);
}
if (f[mask][pre] !== -1) {
return f[mask][pre];
}
let res = Infinity;
for (let cur = 1; cur < n; ++cur) {
if (((mask >> cur) & 1) ^ 1) {
res = Math.min(res, Math.abs(pre - nums[cur]) + dfs(mask | (1 << cur), cur));
}
}
return (f[mask][pre] = res);
};
const g = (mask: number, pre: number) => {
ans.push(pre);
if (mask === (1 << n) - 1) {
return;
}
const res = dfs(mask, pre);
for (let cur = 1; cur < n; ++cur) {
if (((mask >> cur) & 1) ^ 1) {
if (Math.abs(pre - nums[cur]) + dfs(mask | (1 << cur), cur) === res) {
g(mask | (1 << cur), cur);
break;
}
}
}
};
g(1, 0);
return ans;
}
|




