二叉树
哈希表
广度优先搜索
排序
树
深度优先搜索
题目描述
给你一个二叉树的根结点,返回其结点按 垂直方向 (从上到下,逐列)遍历的结果。
如果两个结点在同一行和列,那么顺序则为 从左到右 。
示例 1:
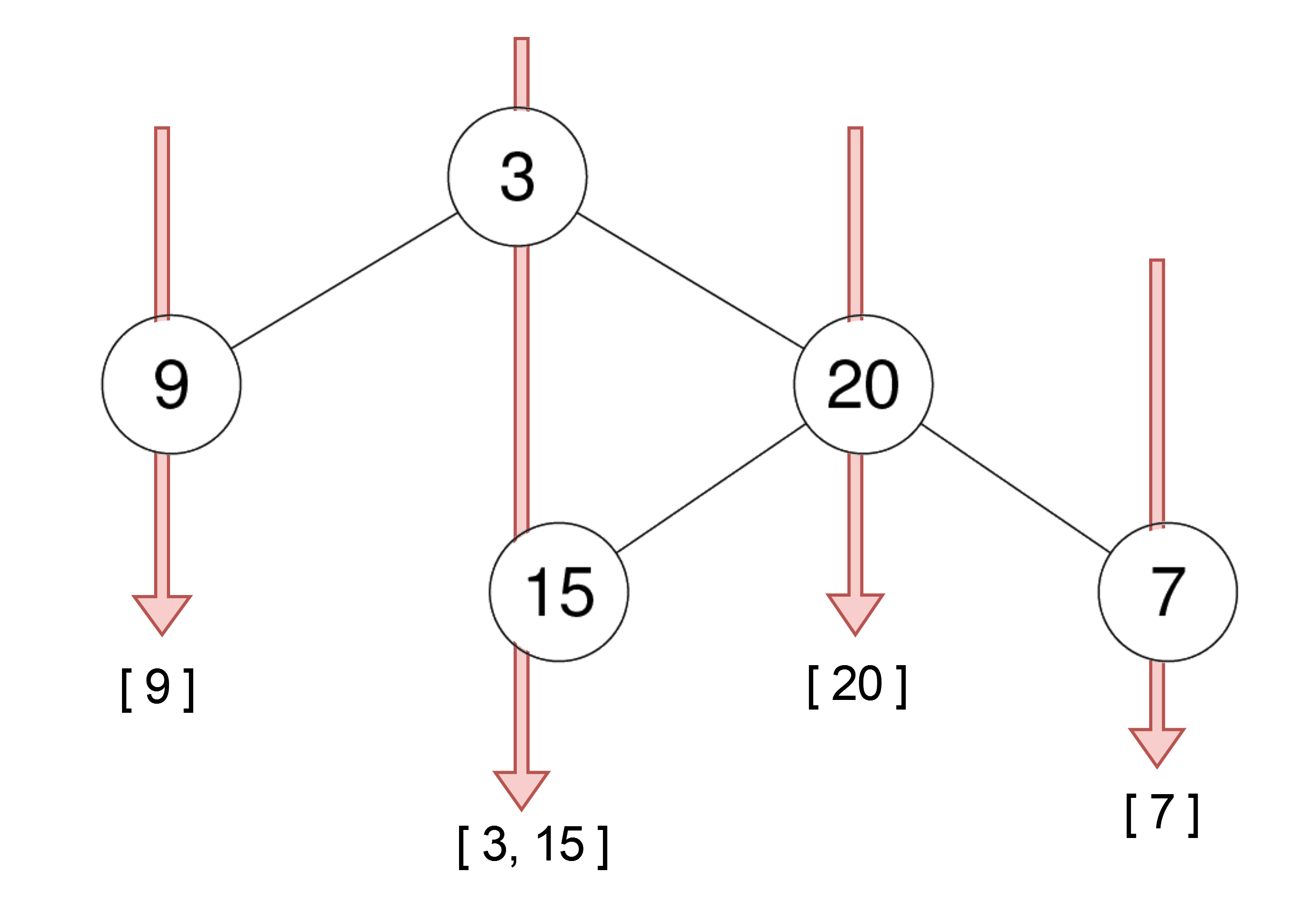
输入: root = [3,9,20,null,null,15,7]
输出: [[9],[3,15],[20],[7]]
示例 2:
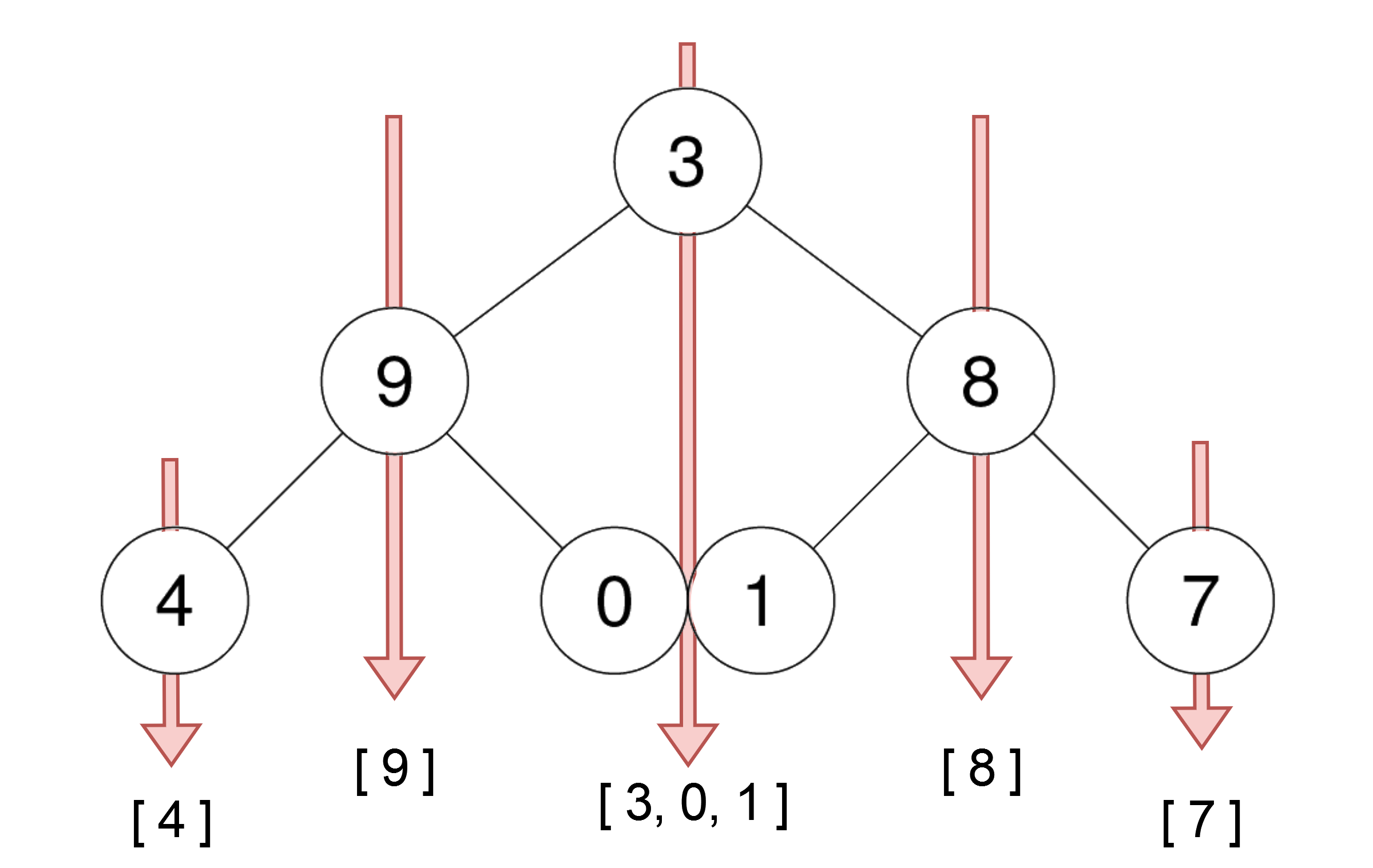
输入: root = [3,9,8,4,0,1,7]
输出: [[4],[9],[3,0,1],[8],[7]]
示例 3:
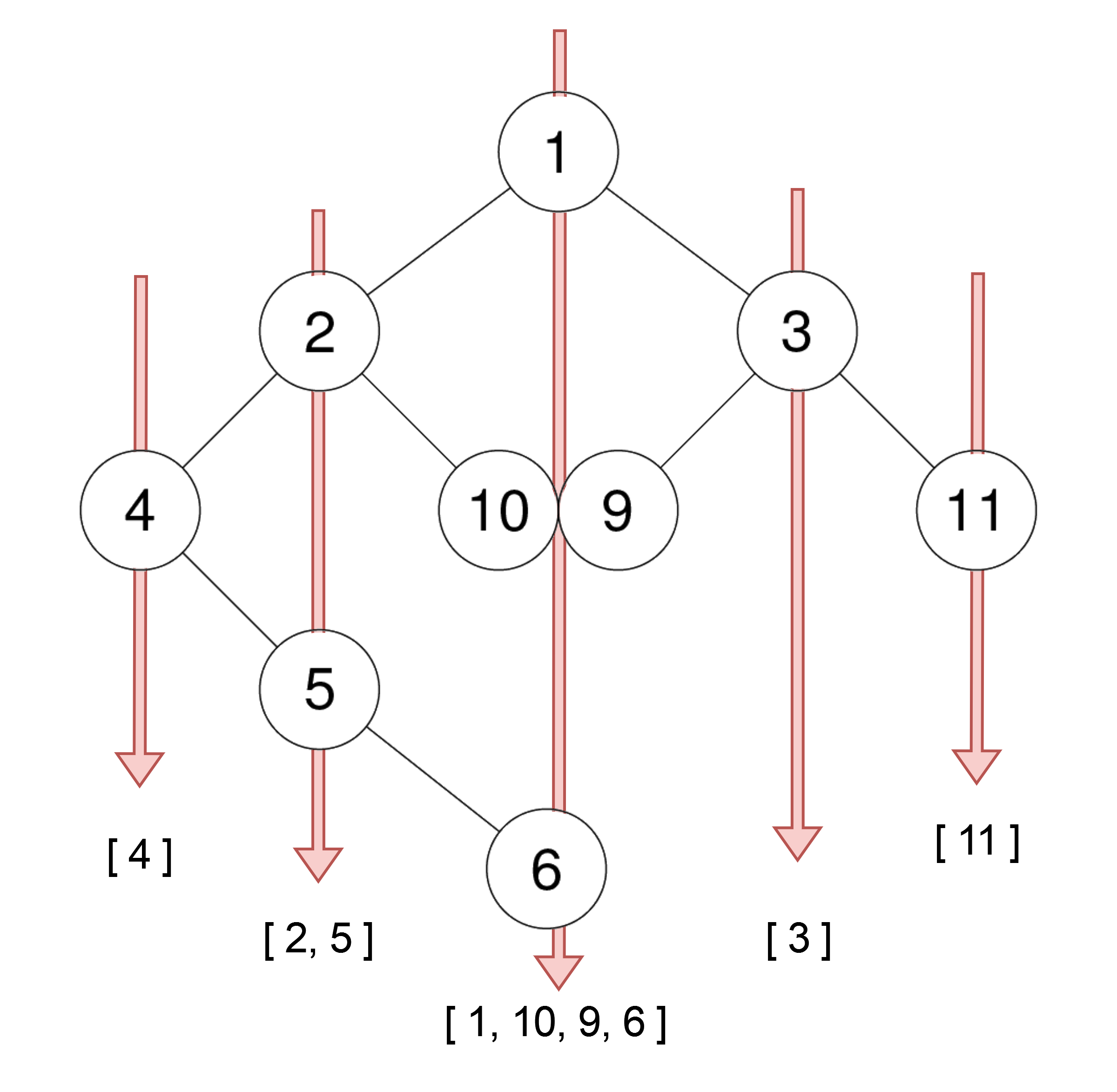
输入: root = [1,2,3,4,10,9,11,null,5,null,null,null,null,null,null,null,6]
输出: [[4],[2,5],[1,10,9,6],[3],[11]]
提示:
树中结点的数目在范围 [0, 100] 内
-100 <= Node.val <= 100
解法
方法一:DFS
DFS 遍历二叉树,记录每个节点的值、深度,以及横向的偏移量。然后对所有节点按照横向偏移量从小到大排序,再按照深度从小到大排序,最后按照横向偏移量分组。
时间复杂度 \(O(n\log \log n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 为二叉树的节点个数。
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def verticalOrder ( self , root : Optional [ TreeNode ]) -> List [ List [ int ]]:
def dfs ( root , depth , offset ):
if root is None :
return
d [ offset ] . append (( depth , root . val ))
dfs ( root . left , depth + 1 , offset - 1 )
dfs ( root . right , depth + 1 , offset + 1 )
d = defaultdict ( list )
dfs ( root , 0 , 0 )
ans = []
for _ , v in sorted ( d . items ()):
v . sort ( key = lambda x : x [ 0 ])
ans . append ([ x [ 1 ] for x in v ])
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private TreeMap < Integer , List < int []>> d = new TreeMap <> ();
public List < List < Integer >> verticalOrder ( TreeNode root ) {
dfs ( root , 0 , 0 );
List < List < Integer >> ans = new ArrayList <> ();
for ( var v : d . values ()) {
Collections . sort ( v , ( a , b ) -> a [ 0 ] - b [ 0 ] );
List < Integer > t = new ArrayList <> ();
for ( var e : v ) {
t . add ( e [ 1 ] );
}
ans . add ( t );
}
return ans ;
}
private void dfs ( TreeNode root , int depth , int offset ) {
if ( root == null ) {
return ;
}
d . computeIfAbsent ( offset , k -> new ArrayList <> ()). add ( new int [] { depth , root . val });
dfs ( root . left , depth + 1 , offset - 1 );
dfs ( root . right , depth + 1 , offset + 1 );
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
using pii = pair < int , int > ;
class Solution {
public :
map < int , vector < pii >> d ;
vector < vector < int >> verticalOrder ( TreeNode * root ) {
dfs ( root , 0 , 0 );
vector < vector < int >> ans ;
for ( auto & [ _ , v ] : d ) {
sort ( v . begin (), v . end (), [ & ]( pii & a , pii & b ) {
return a . first < b . first ;
});
vector < int > t ;
for ( auto & x : v ) {
t . push_back ( x . second );
}
ans . push_back ( t );
}
return ans ;
}
void dfs ( TreeNode * root , int depth , int offset ) {
if ( ! root ) return ;
d [ offset ]. push_back ({ depth , root -> val });
dfs ( root -> left , depth + 1 , offset - 1 );
dfs ( root -> right , depth + 1 , offset + 1 );
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func verticalOrder ( root * TreeNode ) [][] int {
d := map [ int ][][] int {}
var dfs func ( * TreeNode , int , int )
dfs = func ( root * TreeNode , depth , offset int ) {
if root == nil {
return
}
d [ offset ] = append ( d [ offset ], [] int { depth , root . Val })
dfs ( root . Left , depth + 1 , offset - 1 )
dfs ( root . Right , depth + 1 , offset + 1 )
}
dfs ( root , 0 , 0 )
idx := [] int {}
for i := range d {
idx = append ( idx , i )
}
sort . Ints ( idx )
ans := [][] int {}
for _ , i := range idx {
v := d [ i ]
sort . SliceStable ( v , func ( i , j int ) bool { return v [ i ][ 0 ] < v [ j ][ 0 ] })
t := [] int {}
for _ , x := range v {
t = append ( t , x [ 1 ])
}
ans = append ( ans , t )
}
return ans
}
方法二:BFS
本题较好的做法应该是 BFS,从上往下逐层进行遍历。
时间复杂度 \(O(n\log n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 是二叉树的结点数。
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def verticalOrder ( self , root : Optional [ TreeNode ]) -> List [ List [ int ]]:
if root is None :
return []
q = deque ([( root , 0 )])
d = defaultdict ( list )
while q :
for _ in range ( len ( q )):
root , offset = q . popleft ()
d [ offset ] . append ( root . val )
if root . left :
q . append (( root . left , offset - 1 ))
if root . right :
q . append (( root . right , offset + 1 ))
return [ v for _ , v in sorted ( d . items ())]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List < List < Integer >> verticalOrder ( TreeNode root ) {
List < List < Integer >> ans = new ArrayList <> ();
if ( root == null ) {
return ans ;
}
Deque < Pair < TreeNode , Integer >> q = new ArrayDeque <> ();
q . offer ( new Pair <> ( root , 0 ));
TreeMap < Integer , List < Integer >> d = new TreeMap <> ();
while ( ! q . isEmpty ()) {
for ( int n = q . size (); n > 0 ; -- n ) {
var p = q . pollFirst ();
root = p . getKey ();
int offset = p . getValue ();
d . computeIfAbsent ( offset , k -> new ArrayList ()). add ( root . val );
if ( root . left != null ) {
q . offer ( new Pair <> ( root . left , offset - 1 ));
}
if ( root . right != null ) {
q . offer ( new Pair <> ( root . right , offset + 1 ));
}
}
}
return new ArrayList <> ( d . values ());
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
vector < vector < int >> verticalOrder ( TreeNode * root ) {
vector < vector < int >> ans ;
if ( ! root ) return ans ;
map < int , vector < int >> d ;
queue < pair < TreeNode * , int >> q {{{ root , 0 }}};
while ( ! q . empty ()) {
for ( int n = q . size (); n ; -- n ) {
auto p = q . front ();
q . pop ();
root = p . first ;
int offset = p . second ;
d [ offset ]. push_back ( root -> val );
if ( root -> left ) q . push ({ root -> left , offset - 1 });
if ( root -> right ) q . push ({ root -> right , offset + 1 });
}
}
for ( auto & [ _ , v ] : d ) {
ans . push_back ( v );
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func verticalOrder ( root * TreeNode ) [][] int {
ans := [][] int {}
if root == nil {
return ans
}
d := map [ int ][] int {}
q := [] pair { pair { root , 0 }}
for len ( q ) > 0 {
for n := len ( q ); n > 0 ; n -- {
p := q [ 0 ]
q = q [ 1 :]
root = p . node
offset := p . offset
d [ offset ] = append ( d [ offset ], root . Val )
if root . Left != nil {
q = append ( q , pair { root . Left , offset - 1 })
}
if root . Right != nil {
q = append ( q , pair { root . Right , offset + 1 })
}
}
}
idx := [] int {}
for i := range d {
idx = append ( idx , i )
}
sort . Ints ( idx )
for _ , i := range idx {
ans = append ( ans , d [ i ])
}
return ans
}
type pair struct {
node * TreeNode
offset int
}
GitHub