3071. 在矩阵上写出字母 Y 所需的最少操作次数

题目描述

给你一个下标从 0 开始、大小为 n x n 的矩阵 grid ，其中 n 为奇数，且 grid[r][c] 的值为 0 、1 或 2 。

如果一个单元格属于以下三条线中的任一一条，我们就认为它是字母 Y 的一部分：

从左上角单元格开始到矩阵中心单元格结束的对角线。
从右上角单元格开始到矩阵中心单元格结束的对角线。
从中心单元格开始到矩阵底部边界结束的垂直线。

当且仅当满足以下全部条件时，可以判定矩阵上写有字母 Y ：

属于 Y 的所有单元格的值相等。
不属于 Y 的所有单元格的值相等。
属于 Y 的单元格的值与不属于Y的单元格的值不同。

每次操作你可以将任意单元格的值改变为 0 、1 或 2 。返回在矩阵上写出字母 Y 所需的最少操作次数。

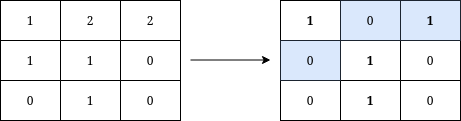
示例 1：

输入：grid = [[1,2,2],[1,1,0],[0,1,0]]
输出：3
解释：将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后，所有属于 Y 的单元格（加粗显示）的值都为 1 ，而不属于 Y 的单元格的值都为 0 。
可以证明，写出 Y 至少需要进行 3 次操作。

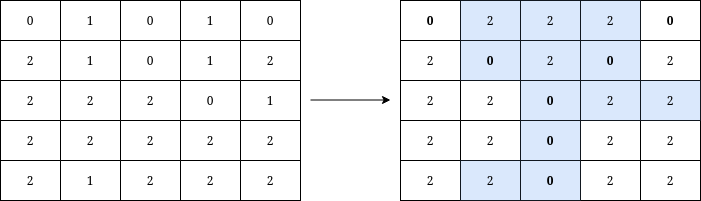
示例 2：

输入：grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]]
输出：12
解释：将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后，所有属于 Y 的单元格（加粗显示）的值都为 0 ，而不属于 Y 的单元格的值都为 2 。
可以证明，写出 Y 至少需要进行 12 次操作。

提示：

3 <= n <= 49
n == grid.length == grid[i].length
0 <= grid[i][j] <= 2
n 为奇数。

解法

方法一：计数

我们用两个长度为 $3$ 的数组 cnt1 和 cnt2 分别记录属于 Y 的单元格和不属于 Y 的单元格的值的个数。然后我们枚举 i 和 j，分别表示属于 Y 的单元格和不属于 Y 的单元格的值，计算出最少操作次数。

时间复杂度 $O(n^2)$，其中 $n$ 是矩阵的大小。空间复杂度 $O(1)$。

Python3JavaC++GoTypeScript

class Solution:
    def minimumOperationsToWriteY(self, grid: List[List[int]]) -> int:
        n = len(grid)
        cnt1 = Counter()
        cnt2 = Counter()
        for i, row in enumerate(grid):
            for j, x in enumerate(row):
                a = i == j and i <= n // 2
                b = i + j == n - 1 and i <= n // 2
                c = j == n // 2 and i >= n // 2
                if a or b or c:
                    cnt1[x] += 1
                else:
                    cnt2[x] += 1
        return min(
            n * n - cnt1[i] - cnt2[j] for i in range(3) for j in range(3) if i != j
        )

class Solution {
    public int minimumOperationsToWriteY(int[][] grid) {
        int n = grid.length;
        int[] cnt1 = new int[3];
        int[] cnt2 = new int[3];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                boolean a = i == j && i <= n / 2;
                boolean b = i + j == n - 1 && i <= n / 2;
                boolean c = j == n / 2 && i >= n / 2;
                if (a || b || c) {
                    ++cnt1[grid[i][j]];
                } else {
                    ++cnt2[grid[i][j]];
                }
            }
        }
        int ans = n * n;
        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                if (i != j) {
                    ans = Math.min(ans, n * n - cnt1[i] - cnt2[j]);
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    int minimumOperationsToWriteY(vector<vector<int>>& grid) {
        int n = grid.size();
        int cnt1[3]{};
        int cnt2[3]{};
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                bool a = i == j && i <= n / 2;
                bool b = i + j == n - 1 && i <= n / 2;
                bool c = j == n / 2 && i >= n / 2;
                if (a || b || c) {
                    ++cnt1[grid[i][j]];
                } else {
                    ++cnt2[grid[i][j]];
                }
            }
        }
        int ans = n * n;
        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                if (i != j) {
                    ans = min(ans, n * n - cnt1[i] - cnt2[j]);
                }
            }
        }
        return ans;
    }
};

func minimumOperationsToWriteY(grid [][]int) int {
    n := len(grid)
    cnt1 := [3]int{}
    cnt2 := [3]int{}
    for i, row := range grid {
        for j, x := range row {
            a := i == j && i <= n/2
            b := i+j == n-1 && i <= n/2
            c := j == n/2 && i >= n/2
            if a || b || c {
                cnt1[x]++
            } else {
                cnt2[x]++
            }
        }
    }
    ans := n * n
    for i := 0; i < 3; i++ {
        for j := 0; j < 3; j++ {
            if i != j {
                ans = min(ans, n*n-cnt1[i]-cnt2[j])
            }
        }
    }
    return ans
}

function minimumOperationsToWriteY(grid: number[][]): number {
    const n = grid.length;
    const cnt1: number[] = Array(3).fill(0);
    const cnt2: number[] = Array(3).fill(0);
    for (let i = 0; i < n; ++i) {
        for (let j = 0; j < n; ++j) {
            const a = i === j && i <= n >> 1;
            const b = i + j === n - 1 && i <= n >> 1;
            const c = j === n >> 1 && i >= n >> 1;
            if (a || b || c) {
                ++cnt1[grid[i][j]];
            } else {
                ++cnt2[grid[i][j]];
            }
        }
    }
    let ans = n * n;
    for (let i = 0; i < 3; ++i) {
        for (let j = 0; j < 3; ++j) {
            if (i !== j) {
                ans = Math.min(ans, n * n - cnt1[i] - cnt2[j]);
            }
        }
    }
    return ans;
}

3071. 在矩阵上写出字母 Y 所需的最少操作次数

题目描述

解法

方法一：计数

评论