3067. 在带权树网络中统计可连接服务器对数目

题目描述

给你一棵无根带权树，树中总共有 n 个节点，分别表示 n 个服务器，服务器从 0 到 n - 1 编号。同时给你一个数组 edges ，其中 edges[i] = [a_i, b_i, weight_i] 表示节点 a_i 和 b_i 之间有一条双向边，边的权值为 weight_i 。再给你一个整数 signalSpeed 。

如果两台服务器 a 和 b 是通过服务器 c 可连接的，则：

a < b ，a != c 且 b != c 。
从 c 到 a 的距离是可以被 signalSpeed 整除的。
从 c 到 b 的距离是可以被 signalSpeed 整除的。
从 c 到 b 的路径与从 c 到 a 的路径没有任何公共边。

请你返回一个长度为 n 的整数数组 count ，其中 count[i] 表示通过服务器 i 可连接 的服务器对的数目。

示例 1：

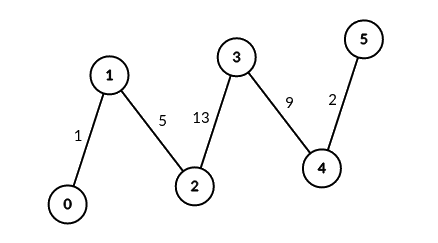
输入：edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1
输出：[0,4,6,6,4,0]
解释：由于 signalSpeed 等于 1 ，count[c] 等于所有从 c 开始且没有公共边的路径对数目。
在输入图中，count[c] 等于服务器 c 左边服务器数目乘以右边服务器数目。

示例 2：

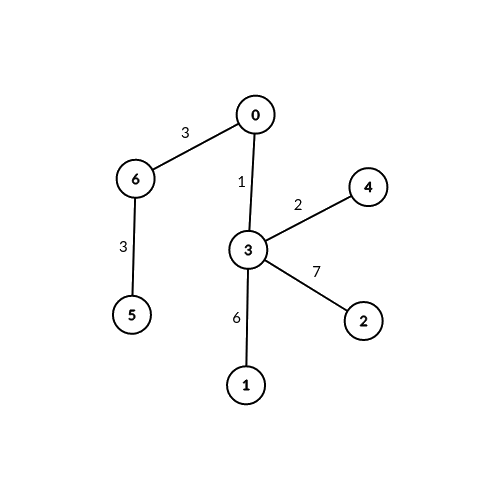
输入：edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3
输出：[2,0,0,0,0,0,2]
解释：通过服务器 0 ，有 2 个可连接服务器对(4, 5) 和 (4, 6) 。
通过服务器 6 ，有 2 个可连接服务器对 (4, 5) 和 (0, 5) 。
所有服务器对都必须通过服务器 0 或 6 才可连接，所以其他服务器对应的可连接服务器对数目都为 0 。

提示：

2 <= n <= 1000
edges.length == n - 1
edges[i].length == 3
0 <= a_i, b_i < n
edges[i] = [a_i, b_i, weight_i]
1 <= weight_i <= 10⁶
1 <= signalSpeed <= 10⁶
输入保证 edges 构成一棵合法的树。

解法

方法一：枚举 + DFS

我们先根据题目给定的边构建出一个邻接表 $g$，其中 $g[a]$ 表示节点 $a$ 的所有邻居节点以及对应的边权。

然后，我们可以枚举每一个节点 $a$ 作为连接的中间节点，通过深度优先搜索计算出从 $a$ 的邻居节点 $b$ 出发的，且到节点 $a$ 的距离可以被 $signalSpeed$ 整除的节点数 $t$。那么，节点 $a$ 的可连接节点对数目增加了 $s \times t$，其中 $s$ 表示节点 $a$ 的邻居节点 $b$ 出发的，且到节点 $a$ 的距离不可以被 $signalSpeed$ 整除的累计节点数。然后我们更新 $s$ 为 $s + t$。

枚举完所有节点 $a$ 之后，我们就可以得到所有节点的可连接节点对数目。

时间复杂度 $O(n^2)$，空间复杂度 $O(n)$。其中 $n$ 表示节点数。

Python3JavaC++GoTypeScript

class Solution:
    def countPairsOfConnectableServers(
        self, edges: List[List[int]], signalSpeed: int
    ) -> List[int]:
        def dfs(a: int, fa: int, ws: int) -> int:
            cnt = 0 if ws % signalSpeed else 1
            for b, w in g[a]:
                if b != fa:
                    cnt += dfs(b, a, ws + w)
            return cnt

        n = len(edges) + 1
        g = [[] for _ in range(n)]
        for a, b, w in edges:
            g[a].append((b, w))
            g[b].append((a, w))
        ans = [0] * n
        for a in range(n):
            s = 0
            for b, w in g[a]:
                t = dfs(b, a, w)
                ans[a] += s * t
                s += t
        return ans

class Solution {
    private int signalSpeed;
    private List<int[]>[] g;

    public int[] countPairsOfConnectableServers(int[][] edges, int signalSpeed) {
        int n = edges.length + 1;
        g = new List[n];
        this.signalSpeed = signalSpeed;
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1], w = e[2];
            g[a].add(new int[] {b, w});
            g[b].add(new int[] {a, w});
        }
        int[] ans = new int[n];
        for (int a = 0; a < n; ++a) {
            int s = 0;
            for (var e : g[a]) {
                int b = e[0], w = e[1];
                int t = dfs(b, a, w);
                ans[a] += s * t;
                s += t;
            }
        }
        return ans;
    }

    private int dfs(int a, int fa, int ws) {
        int cnt = ws % signalSpeed == 0 ? 1 : 0;
        for (var e : g[a]) {
            int b = e[0], w = e[1];
            if (b != fa) {
                cnt += dfs(b, a, ws + w);
            }
        }
        return cnt;
    }
}

class Solution {
public:
    vector<int> countPairsOfConnectableServers(vector<vector<int>>& edges, int signalSpeed) {
        int n = edges.size() + 1;
        vector<pair<int, int>> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1], w = e[2];
            g[a].emplace_back(b, w);
            g[b].emplace_back(a, w);
        }
        function<int(int, int, int)> dfs = [&](int a, int fa, int ws) {
            int cnt = ws % signalSpeed == 0;
            for (auto& [b, w] : g[a]) {
                if (b != fa) {
                    cnt += dfs(b, a, ws + w);
                }
            }
            return cnt;
        };
        vector<int> ans(n);
        for (int a = 0; a < n; ++a) {
            int s = 0;
            for (auto& [b, w] : g[a]) {
                int t = dfs(b, a, w);
                ans[a] += s * t;
                s += t;
            }
        }
        return ans;
    }
};

func countPairsOfConnectableServers(edges [][]int, signalSpeed int) []int {
    n := len(edges) + 1
    type pair struct{ x, w int }
    g := make([][]pair, n)
    for _, e := range edges {
        a, b, w := e[0], e[1], e[2]
        g[a] = append(g[a], pair{b, w})
        g[b] = append(g[b], pair{a, w})
    }
    var dfs func(a, fa, ws int) int
    dfs = func(a, fa, ws int) int {
        cnt := 0
        if ws%signalSpeed == 0 {
            cnt++
        }
        for _, e := range g[a] {
            b, w := e.x, e.w
            if b != fa {
                cnt += dfs(b, a, ws+w)
            }
        }
        return cnt
    }
    ans := make([]int, n)
    for a := 0; a < n; a++ {
        s := 0
        for _, e := range g[a] {
            b, w := e.x, e.w
            t := dfs(b, a, w)
            ans[a] += s * t
            s += t
        }
    }
    return ans
}

function countPairsOfConnectableServers(edges: number[][], signalSpeed: number): number[] {
    const n = edges.length + 1;
    const g: [number, number][][] = Array.from({ length: n }, () => []);
    for (const [a, b, w] of edges) {
        g[a].push([b, w]);
        g[b].push([a, w]);
    }
    const dfs = (a: number, fa: number, ws: number): number => {
        let cnt = ws % signalSpeed === 0 ? 1 : 0;
        for (const [b, w] of g[a]) {
            if (b != fa) {
                cnt += dfs(b, a, ws + w);
            }
        }
        return cnt;
    };
    const ans: number[] = Array(n).fill(0);
    for (let a = 0; a < n; ++a) {
        let s = 0;
        for (const [b, w] of g[a]) {
            const t = dfs(b, a, w);
            ans[a] += s * t;
            s += t;
        }
    }
    return ans;
}

3067. 在带权树网络中统计可连接服务器对数目

题目描述

解法

方法一：枚举 + DFS

评论