


题目描述
给你一个大小为 m x n 、下标从 0 开始的二维矩阵 mat 。在每个单元格,你可以按以下方式生成数字:
- 最多有
8 条路径可以选择:东,东南,南,西南,西,西北,北,东北。
- 选择其中一条路径,沿着这个方向移动,并且将路径上的数字添加到正在形成的数字后面。
- 注意,每一步都会生成数字,例如,如果路径上的数字是
1, 9, 1,那么在这个方向上会生成三个数字:1, 19, 191 。
返回在遍历矩阵所创建的所有数字中,出现频率最高的、大于 10的质数;如果不存在这样的质数,则返回 -1 。如果存在多个出现频率最高的质数,那么返回其中最大的那个。
注意:移动过程中不允许改变方向。
示例 1:
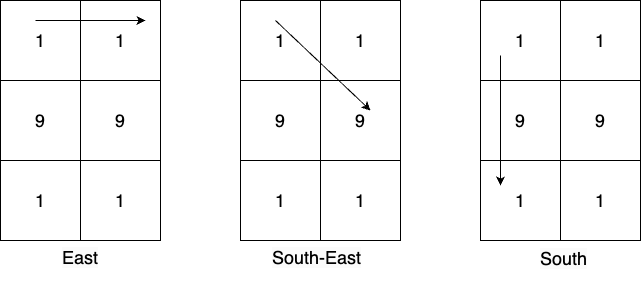
输入:mat = [[1,1],[9,9],[1,1]]
输出:19
解释:
从单元格 (0,0) 出发,有 3 个可能的方向,这些方向上可以生成的大于 10 的数字有:
东方向: [11], 东南方向: [19], 南方向: [19,191] 。
从单元格 (0,1) 出发,所有可能方向上生成的大于 10 的数字有:[19,191,19,11] 。
从单元格 (1,0) 出发,所有可能方向上生成的大于 10 的数字有:[99,91,91,91,91] 。
从单元格 (1,1) 出发,所有可能方向上生成的大于 10 的数字有:[91,91,99,91,91] 。
从单元格 (2,0) 出发,所有可能方向上生成的大于 10 的数字有:[11,19,191,19] 。
从单元格 (2,1) 出发,所有可能方向上生成的大于 10 的数字有:[11,19,19,191] 。
在所有生成的数字中,出现频率最高的质数是 19 。
示例 2:
输入:mat = [[7]]
输出:-1
解释:唯一可以生成的数字是 7 。它是一个质数,但不大于 10 ,所以返回 -1 。
示例 3:
输入:mat = [[9,7,8],[4,6,5],[2,8,6]]
输出:97
解释:
从单元格 (0,0) 出发,所有可能方向上生成的大于 10 的数字有: [97,978,96,966,94,942] 。
从单元格 (0,1) 出发,所有可能方向上生成的大于 10 的数字有: [78,75,76,768,74,79] 。
从单元格 (0,2) 出发,所有可能方向上生成的大于 10 的数字有: [85,856,86,862,87,879] 。
从单元格 (1,0) 出发,所有可能方向上生成的大于 10 的数字有: [46,465,48,42,49,47] 。
从单元格 (1,1) 出发,所有可能方向上生成的大于 10 的数字有: [65,66,68,62,64,69,67,68] 。
从单元格 (1,2) 出发,所有可能方向上生成的大于 10 的数字有: [56,58,56,564,57,58] 。
从单元格 (2,0) 出发,所有可能方向上生成的大于 10 的数字有: [28,286,24,249,26,268] 。
从单元格 (2,1) 出发,所有可能方向上生成的大于 10 的数字有: [86,82,84,86,867,85] 。
从单元格 (2,2) 出发,所有可能方向上生成的大于 10 的数字有: [68,682,66,669,65,658] 。
在所有生成的数字中,出现频率最高的质数是 97 。
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 61 <= mat[i][j] <= 9
解法
方法一:哈希表 + 枚举
我们可以使用哈希表来统计每个大于 10 的素数出现的次数。
对于每个单元格,我们可以从它出发,沿着 8 个方向之一生成数字,然后判断生成的数字是否是大于 \(10\) 的素数,如果是的话,就将它加入到哈希表中。
最后,我们遍历哈希表,找到出现频率最高的质数,如果有多个出现频率最高的质数,那么返回其中最大的那个。
时间复杂度 \(O(m \times n \times \max(m, n) \times {10}^{\frac{\max(m, n)}{2}})\),空间复杂度 \(O(m \times n \times \max(m, n))\)。其中 \(m\) 和 \(n\) 分别是 mat 的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution:
def mostFrequentPrime(self, mat: List[List[int]]) -> int:
def is_prime(x: int) -> int:
return all(x % i != 0 for i in range(2, isqrt(x) + 1))
m, n = len(mat), len(mat[0])
cnt = Counter()
for i in range(m):
for j in range(n):
for a in range(-1, 2):
for b in range(-1, 2):
if a == 0 and b == 0:
continue
x, y, v = i + a, j + b, mat[i][j]
while 0 <= x < m and 0 <= y < n:
v = v * 10 + mat[x][y]
if is_prime(v):
cnt[v] += 1
x, y = x + a, y + b
ans, mx = -1, 0
for v, x in cnt.items():
if mx < x:
mx = x
ans = v
elif mx == x:
ans = max(ans, v)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44 | class Solution {
public int mostFrequentPrime(int[][] mat) {
int m = mat.length, n = mat[0].length;
Map<Integer, Integer> cnt = new HashMap<>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int a = -1; a <= 1; ++a) {
for (int b = -1; b <= 1; ++b) {
if (a == 0 && b == 0) {
continue;
}
int x = i + a, y = j + b, v = mat[i][j];
while (x >= 0 && x < m && y >= 0 && y < n) {
v = v * 10 + mat[x][y];
if (isPrime(v)) {
cnt.merge(v, 1, Integer::sum);
}
x += a;
y += b;
}
}
}
}
}
int ans = -1, mx = 0;
for (var e : cnt.entrySet()) {
int v = e.getKey(), x = e.getValue();
if (mx < x || (mx == x && ans < v)) {
mx = x;
ans = v;
}
}
return ans;
}
private boolean isPrime(int n) {
for (int i = 2; i <= n / i; ++i) {
if (n % i == 0) {
return false;
}
}
return true;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 | class Solution {
public:
int mostFrequentPrime(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
unordered_map<int, int> cnt;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int a = -1; a <= 1; ++a) {
for (int b = -1; b <= 1; ++b) {
if (a == 0 && b == 0) {
continue;
}
int x = i + a, y = j + b, v = mat[i][j];
while (x >= 0 && x < m && y >= 0 && y < n) {
v = v * 10 + mat[x][y];
if (isPrime(v)) {
cnt[v]++;
}
x += a;
y += b;
}
}
}
}
}
int ans = -1, mx = 0;
for (auto& [v, x] : cnt) {
if (mx < x || (mx == x && ans < v)) {
mx = x;
ans = v;
}
}
return ans;
}
private:
bool isPrime(int n) {
for (int i = 2; i <= n / i; ++i) {
if (n % i == 0) {
return false;
}
}
return true;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | func mostFrequentPrime(mat [][]int) int {
m, n := len(mat), len(mat[0])
cnt := make(map[int]int)
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
for a := -1; a <= 1; a++ {
for b := -1; b <= 1; b++ {
if a == 0 && b == 0 {
continue
}
x, y, v := i+a, j+b, mat[i][j]
for x >= 0 && x < m && y >= 0 && y < n {
v = v*10 + mat[x][y]
if isPrime(v) {
cnt[v]++
}
x += a
y += b
}
}
}
}
}
ans, mx := -1, 0
for v, x := range cnt {
if mx < x || (mx == x && ans < v) {
mx = x
ans = v
}
}
return ans
}
func isPrime(n int) bool {
for i := 2; i <= n/i; i++ {
if n%i == 0 {
return false
}
}
return true
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 | function mostFrequentPrime(mat: number[][]): number {
const m: number = mat.length;
const n: number = mat[0].length;
const cnt: Map<number, number> = new Map();
const isPrime = (x: number): boolean => {
for (let i = 2; i <= x / i; ++i) {
if (x % i === 0) {
return false;
}
}
return true;
};
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
for (let a = -1; a <= 1; ++a) {
for (let b = -1; b <= 1; ++b) {
if (a === 0 && b === 0) {
continue;
}
let [x, y, v] = [i + a, j + b, mat[i][j]];
while (x >= 0 && x < m && y >= 0 && y < n) {
v = v * 10 + mat[x][y];
if (isPrime(v)) {
cnt.set(v, (cnt.get(v) || 0) + 1);
}
x += a;
y += b;
}
}
}
}
}
let [ans, mx] = [-1, 0];
cnt.forEach((x, v) => {
if (mx < x || (mx === x && ans < v)) {
mx = x;
ans = v;
}
});
return ans;
}
|



