3015. 按距离统计房屋对数目 I

题目描述

给你三个 正整数 n 、x 和 y 。

在城市中，存在编号从 1 到 n 的房屋，由 n 条街道相连。对所有 1 <= i < n ，都存在一条街道连接编号为 i 的房屋与编号为 i + 1 的房屋。另存在一条街道连接编号为 x 的房屋与编号为 y 的房屋。

对于每个 k（1 <= k <= n），你需要找出所有满足要求的 房屋对 [house₁, house₂] ，即从 house₁ 到 house₂ 需要经过的最少街道数为 k 。

返回一个下标从 1 开始且长度为 n 的数组 result ，其中 result[k] 表示所有满足要求的房屋对的数量，即从一个房屋到另一个房屋需要经过的最少街道数为 k 。

注意，x 与 y 可以相等。

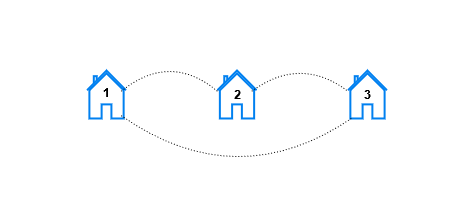
示例 1：

输入：n = 3, x = 1, y = 3
输出：[6,0,0]
解释：让我们检视每个房屋对
- 对于房屋对 (1, 2)，可以直接从房屋 1 到房屋 2。
- 对于房屋对 (2, 1)，可以直接从房屋 2 到房屋 1。
- 对于房屋对 (1, 3)，可以直接从房屋 1 到房屋 3。
- 对于房屋对 (3, 1)，可以直接从房屋 3 到房屋 1。
- 对于房屋对 (2, 3)，可以直接从房屋 2 到房屋 3。
- 对于房屋对 (3, 2)，可以直接从房屋 3 到房屋 2。

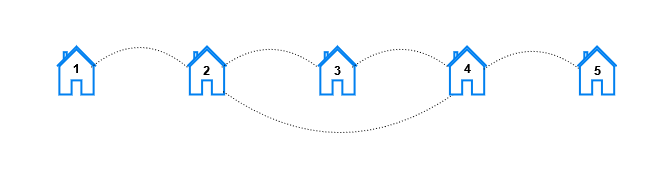
示例 2：

输入：n = 5, x = 2, y = 4
输出：[10,8,2,0,0]
解释：对于每个距离 k ，满足要求的房屋对如下：
- 对于 k == 1，满足要求的房屋对有 (1, 2), (2, 1), (2, 3), (3, 2), (2, 4), (4, 2), (3, 4), (4, 3), (4, 5), 以及 (5, 4)。
- 对于 k == 2，满足要求的房屋对有 (1, 3), (3, 1), (1, 4), (4, 1), (2, 5), (5, 2), (3, 5), 以及 (5, 3)。
- 对于 k == 3，满足要求的房屋对有 (1, 5)，以及 (5, 1) 。
- 对于 k == 4 和 k == 5，不存在满足要求的房屋对。

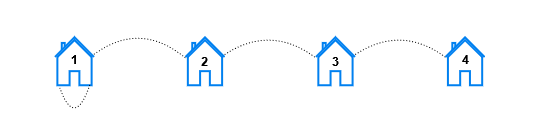
示例 3：

输入：n = 4, x = 1, y = 1
输出：[6,4,2,0]
解释：对于每个距离 k ，满足要求的房屋对如下：
- 对于 k == 1，满足要求的房屋对有 (1, 2), (2, 1), (2, 3), (3, 2), (3, 4), 以及 (4, 3)。
- 对于 k == 2，满足要求的房屋对有 (1, 3), (3, 1), (2, 4), 以及 (4, 2)。
- 对于 k == 3，满足要求的房屋对有 (1, 4), 以及 (4, 1)。
- 对于 k == 4，不存在满足要求的房屋对。

提示：

2 <= n <= 100
1 <= x, y <= n

解法

方法一：枚举

我们可以枚举每个点对 $(i, j)$，那么从 $i$ 到 $j$ 的最短距离为 $min(|i - j|, |i - x| + 1 + |j - y|, |i - y| + 1 + |j - x|)$，我们将该距离的出现次数加 $2$，因为 $(i, j)$ 和 $(j, i)$ 都是满足要求的点对。

时间复杂度 $O(n^2)$，其中 $n$ 是题目给定的 $n$。忽略答案数组的空间消耗，空间复杂度 $O(1)$。

Python3JavaC++GoTypeScript

class Solution:
    def countOfPairs(self, n: int, x: int, y: int) -> List[int]:
        x, y = x - 1, y - 1
        ans = [0] * n
        for i in range(n):
            for j in range(i + 1, n):
                a = j - i
                b = abs(i - x) + 1 + abs(j - y)
                c = abs(i - y) + 1 + abs(j - x)
                ans[min(a, b, c) - 1] += 2
        return ans

class Solution {
    public int[] countOfPairs(int n, int x, int y) {
        int[] ans = new int[n];
        x--;
        y--;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                int a = j - i;
                int b = Math.abs(i - x) + 1 + Math.abs(j - y);
                int c = Math.abs(i - y) + 1 + Math.abs(j - x);
                ans[Math.min(a, Math.min(b, c)) - 1] += 2;
            }
        }
        return ans;
    }
}

class Solution {
public:
    vector<int> countOfPairs(int n, int x, int y) {
        vector<int> ans(n);
        x--;
        y--;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                int a = j - i;
                int b = abs(x - i) + abs(y - j) + 1;
                int c = abs(y - i) + abs(x - j) + 1;
                ans[min({a, b, c}) - 1] += 2;
            }
        }
        return ans;
    }
};

func countOfPairs(n int, x int, y int) []int {
    ans := make([]int, n)
    x, y = x-1, y-1
    for i := 0; i < n; i++ {
        for j := i + 1; j < n; j++ {
            a := j - i
            b := abs(x-i) + abs(y-j) + 1
            c := abs(x-j) + abs(y-i) + 1
            ans[min(a, min(b, c))-1] += 2
        }
    }
    return ans
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

function countOfPairs(n: number, x: number, y: number): number[] {
    const ans: number[] = Array(n).fill(0);
    x--;
    y--;
    for (let i = 0; i < n; ++i) {
        for (let j = i + 1; j < n; ++j) {
            const a = j - i;
            const b = Math.abs(x - i) + Math.abs(y - j) + 1;
            const c = Math.abs(y - i) + Math.abs(x - j) + 1;
            ans[Math.min(a, b, c) - 1] += 2;
        }
    }
    return ans;
}

3015. 按距离统计房屋对数目 I

题目描述

解法

方法一：枚举

评论