跳转至

3009. 折线图上的最大交点数量 🔒

题目描述

有一条由 n 个点连接而成的折线图。给定一个 下标从 1 开始 的整数数组 y，第 k 个点的坐标是 (k, y[k])。图中没有水平线，即没有两个相邻的点有相同的 y 坐标。

假设在图中任意画一条无限长的水平线。请返回这条水平线与折线相交的最多交点数。

 

示例 1：

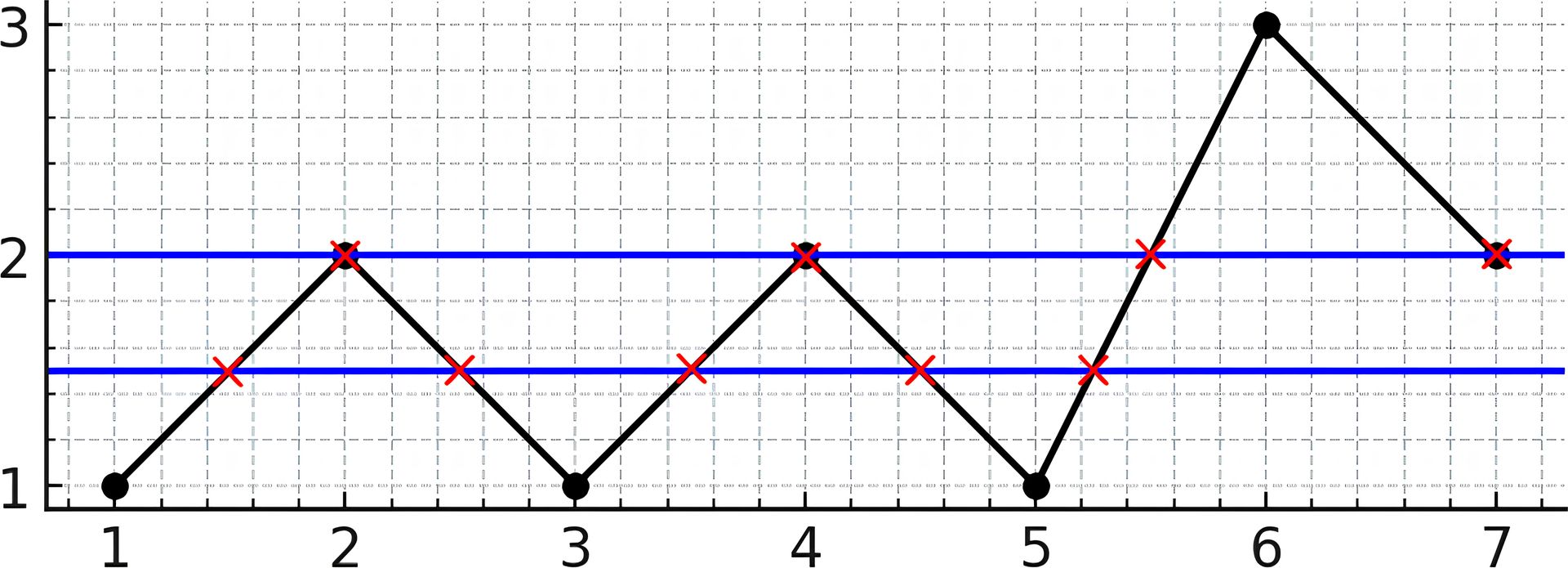
输入：y = [1,2,1,2,1,3,2]
输出：5
解释：如上图所示，水平线 y = 1.5 与折线相交了 5 次（用红叉表示）。水平线 y = 2 与折线相交了 4 次（用红叉表示）。可以证明没有其他水平线可以与折线有超过 5 个点相交。因此，答案是 5。

示例 2：

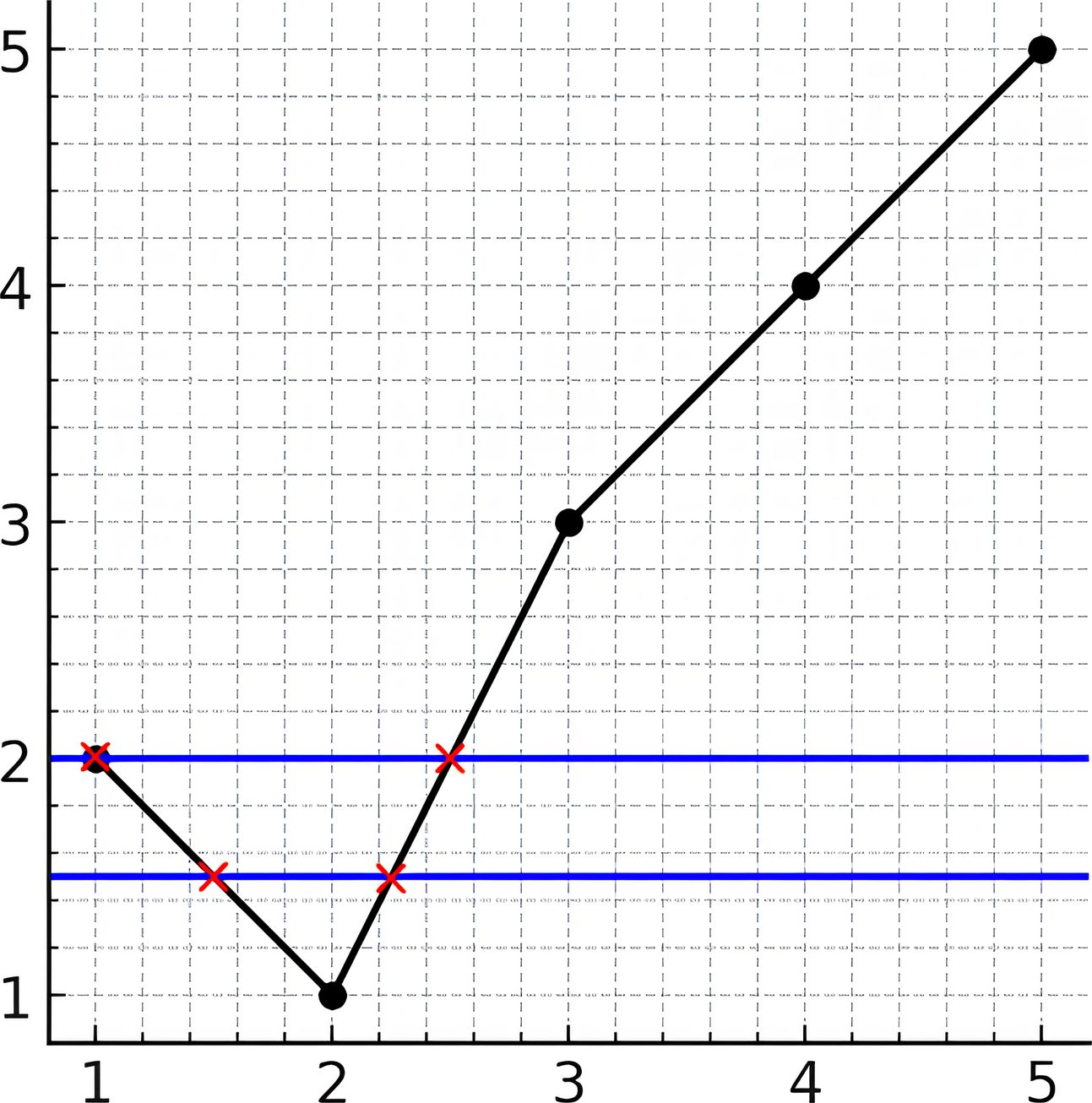
输入：y = [2,1,3,4,5]
输出：2
解释：如上图所示，水平线 y=1.5 与折线相交了 2 次（用红叉表示）。水平线 y=2 与折线相交了 2 次（用红叉表示）。可以证明没有其他水平线可以与折线有超过 2 个点相交。因此，答案是 2。

 

提示：

  • 2 <= y.length <= 105
  • 1 <= y[i] <= 109
  • 对于范围 [1, n - 1] 内的所有 i，都有 y[i] != y[i + 1]

解法

方法一

1


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int maxIntersectionCount(int[] y) {
        final int n = y.length;
        int ans = 0;
        int intersectionCount = 0;
        TreeMap<Integer, Integer> line = new TreeMap<>();

        for (int i = 1; i < n; ++i) {
            final int start = 2 * y[i - 1];
            final int end = 2 * y[i] + (i == n - 1 ? 0 : y[i] > y[i - 1] ? -1 : 1);
            line.merge(Math.min(start, end), 1, Integer::sum);
            line.merge(Math.max(start, end) + 1, -1, Integer::sum);
        }

        for (final int count : line.values()) {
            intersectionCount += count;
            ans = Math.max(ans, intersectionCount);
        }

        return ans;
    }
}

1


1

评论