


题目描述
有一个大型的 (m - 1) x (n - 1) 矩形田地,其两个对角分别是 (1, 1) 和 (m, n) ,田地内部有一些水平栅栏和垂直栅栏,分别由数组 hFences 和 vFences 给出。
水平栅栏为坐标 (hFences[i], 1) 到 (hFences[i], n),垂直栅栏为坐标 (1, vFences[i]) 到 (m, vFences[i]) 。
返回通过 移除 一些栅栏(可能不移除)所能形成的最大面积的 正方形 田地的面积,或者如果无法形成正方形田地则返回 -1。
由于答案可能很大,所以请返回结果对 109 + 7 取余 后的值。
注意:田地外围两个水平栅栏(坐标 (1, 1) 到 (1, n) 和坐标 (m, 1) 到 (m, n) )以及两个垂直栅栏(坐标 (1, 1) 到 (m, 1) 和坐标 (1, n) 到 (m, n) )所包围。这些栅栏 不能 被移除。
示例 1:
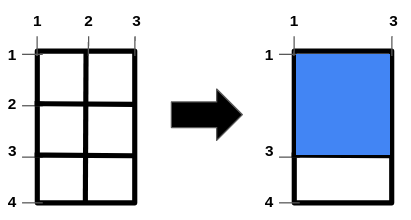
输入:m = 4, n = 3, hFences = [2,3], vFences = [2]
输出:4
解释:移除位于 2 的水平栅栏和位于 2 的垂直栅栏将得到一个面积为 4 的正方形田地。
示例 2:

输入:m = 6, n = 7, hFences = [2], vFences = [4]
输出:-1
解释:可以证明无法通过移除栅栏形成正方形田地。
提示:
3 <= m, n <= 1091 <= hFences.length, vFences.length <= 6001 < hFences[i] < m1 < vFences[i] < nhFences 和 vFences 中的元素是唯一的。
解法
方法一:枚举
我们可以枚举 \(\textit{hFences}\) 中的任意两条水平栅栏 \(a\) 和 \(b\),计算 \(a\) 和 \(b\) 之间的距离 \(d\),记录在哈希表 \(hs\) 中,然后枚举 \(\textit{vFences}\) 中的任意两条垂直栅栏 \(c\) 和 \(d\),计算 \(c\) 和 \(d\) 之间的距离 \(d\),记录在哈希表 \(vs\) 中,最后遍历哈希表 \(hs\),如果 \(hs\) 中的某个距离 \(d\) 在哈希表 \(vs\) 中也存在,那么说明存在一个正方形田地,其边长为 \(d\),面积为 \(d^2\),我们只需要取最大的 \(d\),求 \(d^2 \bmod 10^9 + 7\) 即可。
时间复杂度 \(O(h^2 + v^2)\),空间复杂度 \(O(h^2 + v^2)\)。其中 \(h\) 和 \(v\) 分别是 \(\textit{hFences}\) 和 \(\textit{vFences}\) 的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | class Solution:
def maximizeSquareArea(
self, m: int, n: int, hFences: List[int], vFences: List[int]
) -> int:
def f(nums: List[int], k: int) -> Set[int]:
nums.extend([1, k])
nums.sort()
return {b - a for a, b in combinations(nums, 2)}
mod = 10**9 + 7
hs = f(hFences, m)
vs = f(vFences, n)
ans = max(hs & vs, default=0)
return ans**2 % mod if ans else -1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | class Solution {
public int maximizeSquareArea(int m, int n, int[] hFences, int[] vFences) {
Set<Integer> hs = f(hFences, m);
Set<Integer> vs = f(vFences, n);
hs.retainAll(vs);
int ans = -1;
final int mod = (int) 1e9 + 7;
for (int x : hs) {
ans = Math.max(ans, x);
}
return ans > 0 ? (int) (1L * ans * ans % mod) : -1;
}
private Set<Integer> f(int[] nums, int k) {
int n = nums.length;
nums = Arrays.copyOf(nums, n + 2);
nums[n] = 1;
nums[n + 1] = k;
Arrays.sort(nums);
Set<Integer> s = new HashSet<>();
for (int i = 0; i < nums.length; ++i) {
for (int j = 0; j < i; ++j) {
s.add(nums[i] - nums[j]);
}
}
return s;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
public:
int maximizeSquareArea(int m, int n, vector<int>& hFences, vector<int>& vFences) {
auto f = [](vector<int>& nums, int k) {
nums.push_back(k);
nums.push_back(1);
sort(nums.begin(), nums.end());
unordered_set<int> s;
for (int i = 0; i < nums.size(); ++i) {
for (int j = 0; j < i; ++j) {
s.insert(nums[i] - nums[j]);
}
}
return s;
};
auto hs = f(hFences, m);
auto vs = f(vFences, n);
int ans = 0;
for (int h : hs) {
if (vs.count(h)) {
ans = max(ans, h);
}
}
const int mod = 1e9 + 7;
return ans > 0 ? 1LL * ans * ans % mod : -1;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | func maximizeSquareArea(m int, n int, hFences []int, vFences []int) int {
f := func(nums []int, k int) map[int]bool {
nums = append(nums, 1, k)
sort.Ints(nums)
s := map[int]bool{}
for i := 0; i < len(nums); i++ {
for j := 0; j < i; j++ {
s[nums[i]-nums[j]] = true
}
}
return s
}
hs := f(hFences, m)
vs := f(vFences, n)
ans := 0
for h := range hs {
if vs[h] {
ans = max(ans, h)
}
}
if ans > 0 {
return ans * ans % (1e9 + 7)
}
return -1
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | function maximizeSquareArea(m: number, n: number, hFences: number[], vFences: number[]): number {
const f = (nums: number[], k: number): Set<number> => {
nums.push(1, k);
nums.sort((a, b) => a - b);
const s: Set<number> = new Set();
for (let i = 0; i < nums.length; ++i) {
for (let j = 0; j < i; ++j) {
s.add(nums[i] - nums[j]);
}
}
return s;
};
const hs = f(hFences, m);
const vs = f(vFences, n);
let ans = 0;
for (const h of hs) {
if (vs.has(h)) {
ans = Math.max(ans, h);
}
}
return ans ? Number(BigInt(ans) ** 2n % 1000000007n) : -1;
}
|




