


题目描述
给你一个 n 个点的 简单有向图 (没有重复边的有向图),节点编号为 0 到 n - 1 。如果这些边是双向边,那么这个图形成一棵 树 。
给你一个整数 n 和一个 二维 整数数组 edges ,其中 edges[i] = [ui, vi] 表示从节点 ui 到节点 vi 有一条 有向边 。
边反转 指的是将一条边的方向反转,也就是说一条从节点 ui 到节点 vi 的边会变为一条从节点 vi 到节点 ui 的边。
对于范围 [0, n - 1] 中的每一个节点 i ,你的任务是分别 独立 计算 最少 需要多少次 边反转 ,从节点 i 出发经过 一系列有向边 ,可以到达所有的节点。
请你返回一个长度为 n 的整数数组 answer ,其中 answer[i]表示从节点 i 出发,可以到达所有节点的 最少边反转 次数。
示例 1:
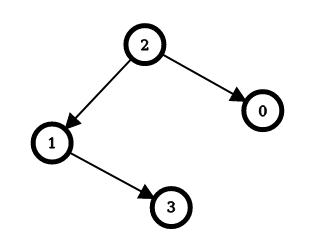
输入:n = 4, edges = [[2,0],[2,1],[1,3]]
输出:[1,1,0,2]
解释:上图表示了与输入对应的简单有向图。
对于节点 0 :反转 [2,0] ,从节点 0 出发可以到达所有节点。
所以 answer[0] = 1 。
对于节点 1 :反转 [2,1] ,从节点 1 出发可以到达所有节点。
所以 answer[1] = 1 。
对于节点 2 :不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[2] = 0 。
对于节点 3 :反转 [1,3] 和 [2,1] ,从节点 3 出发可以到达所有节点。
所以 answer[3] = 2 。
示例 2:
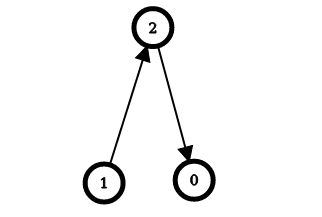
输入:n = 3, edges = [[1,2],[2,0]]
输出:[2,0,1]
解释:上图表示了与输入对应的简单有向图。
对于节点 0 :反转 [2,0] 和 [1,2] ,从节点 0 出发可以到达所有节点。
所以 answer[0] = 2 。
对于节点 1 :不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[1] = 0 。
对于节点 2 :反转 [1,2] ,从节点 2 出发可以到达所有节点。
所以 answer[2] = 1 。
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ui == edges[i][0] < n0 <= vi == edges[i][1] < nui != vi- 输入保证如果边是双向边,可以得到一棵树。
解法
方法一:树形 DP
时间复杂度 $O(n)$,空间复杂度 $O(n)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | class Solution:
def minEdgeReversals(self, n: int, edges: List[List[int]]) -> List[int]:
ans = [0] * n
g = [[] for _ in range(n)]
for x, y in edges:
g[x].append((y, 1))
g[y].append((x, -1))
def dfs(i: int, fa: int):
for j, k in g[i]:
if j != fa:
ans[0] += int(k < 0)
dfs(j, i)
dfs(0, -1)
def dfs2(i: int, fa: int):
for j, k in g[i]:
if j != fa:
ans[j] = ans[i] + k
dfs2(j, i)
dfs2(0, -1)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | class Solution {
private List<int[]>[] g;
private int[] ans;
public int[] minEdgeReversals(int n, int[][] edges) {
ans = new int[n];
g = new List[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (var e : edges) {
int x = e[0], y = e[1];
g[x].add(new int[] {y, 1});
g[y].add(new int[] {x, -1});
}
dfs(0, -1);
dfs2(0, -1);
return ans;
}
private void dfs(int i, int fa) {
for (var ne : g[i]) {
int j = ne[0], k = ne[1];
if (j != fa) {
ans[0] += k < 0 ? 1 : 0;
dfs(j, i);
}
}
}
private void dfs2(int i, int fa) {
for (var ne : g[i]) {
int j = ne[0], k = ne[1];
if (j != fa) {
ans[j] = ans[i] + k;
dfs2(j, i);
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | class Solution {
public:
vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) {
vector<pair<int, int>> g[n];
vector<int> ans(n);
for (auto& e : edges) {
int x = e[0], y = e[1];
g[x].emplace_back(y, 1);
g[y].emplace_back(x, -1);
}
function<void(int, int)> dfs = [&](int i, int fa) {
for (auto& [j, k] : g[i]) {
if (j != fa) {
ans[0] += k < 0;
dfs(j, i);
}
}
};
function<void(int, int)> dfs2 = [&](int i, int fa) {
for (auto& [j, k] : g[i]) {
if (j != fa) {
ans[j] = ans[i] + k;
dfs2(j, i);
}
}
};
dfs(0, -1);
dfs2(0, -1);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | func minEdgeReversals(n int, edges [][]int) []int {
g := make([][][2]int, n)
for _, e := range edges {
x, y := e[0], e[1]
g[x] = append(g[x], [2]int{y, 1})
g[y] = append(g[y], [2]int{x, -1})
}
ans := make([]int, n)
var dfs func(int, int)
var dfs2 func(int, int)
dfs = func(i, fa int) {
for _, ne := range g[i] {
j, k := ne[0], ne[1]
if j != fa {
if k < 0 {
ans[0]++
}
dfs(j, i)
}
}
}
dfs2 = func(i, fa int) {
for _, ne := range g[i] {
j, k := ne[0], ne[1]
if j != fa {
ans[j] = ans[i] + k
dfs2(j, i)
}
}
}
dfs(0, -1)
dfs2(0, -1)
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | function minEdgeReversals(n: number, edges: number[][]): number[] {
const g: number[][][] = Array.from({ length: n }, () => []);
for (const [x, y] of edges) {
g[x].push([y, 1]);
g[y].push([x, -1]);
}
const ans: number[] = Array(n).fill(0);
const dfs = (i: number, fa: number) => {
for (const [j, k] of g[i]) {
if (j !== fa) {
ans[0] += k < 0 ? 1 : 0;
dfs(j, i);
}
}
};
const dfs2 = (i: number, fa: number) => {
for (const [j, k] of g[i]) {
if (j !== fa) {
ans[j] = ans[i] + k;
dfs2(j, i);
}
}
};
dfs(0, -1);
dfs2(0, -1);
return ans;
}
|




