


题目描述
给你一棵 树(即,一个连通、无向且无环的图),根 节点为 0 ,由编号从 0 到 n - 1 的 n 个节点组成。这棵树用一个长度为 n 、下标从 0 开始的数组 parent 表示,其中 parent[i] 为节点 i 的父节点,由于节点 0 为根节点,所以 parent[0] == -1 。
另给你一个长度为 n 的字符串 s ,其中 s[i] 是分配给 i 和 parent[i] 之间的边的字符。s[0] 可以忽略。
找出满足 u < v ,且从 u 到 v 的路径上分配的字符可以 重新排列 形成 回文 的所有节点对 (u, v) ,并返回节点对的数目。
如果一个字符串正着读和反着读都相同,那么这个字符串就是一个 回文 。
示例 1:
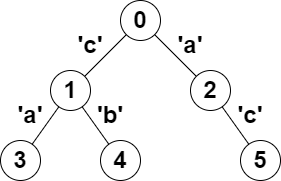
输入:parent = [-1,0,0,1,1,2], s = "acaabc"
输出:8
解释:符合题目要求的节点对分别是:
- (0,1)、(0,2)、(1,3)、(1,4) 和 (2,5) ,路径上只有一个字符,满足回文定义。
- (2,3),路径上字符形成的字符串是 "aca" ,满足回文定义。
- (1,5),路径上字符形成的字符串是 "cac" ,满足回文定义。
- (3,5),路径上字符形成的字符串是 "acac" ,可以重排形成回文 "acca" 。
示例 2:
输入:parent = [-1,0,0,0,0], s = "aaaaa"
输出:10
解释:任何满足 u < v 的节点对 (u,v) 都符合题目要求。
提示:
n == parent.length == s.length1 <= n <= 105- 对于所有
i >= 1 ,0 <= parent[i] <= n - 1 均成立
parent[0] == -1parent 表示一棵有效的树s 仅由小写英文字母组成
解法
方法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution:
def countPalindromePaths(self, parent: List[int], s: str) -> int:
def dfs(i: int, xor: int):
nonlocal ans
for j, v in g[i]:
x = xor ^ v
ans += cnt[x]
for k in range(26):
ans += cnt[x ^ (1 << k)]
cnt[x] += 1
dfs(j, x)
n = len(parent)
g = defaultdict(list)
for i in range(1, n):
p = parent[i]
g[p].append((i, 1 << (ord(s[i]) - ord('a'))))
ans = 0
cnt = Counter({0: 1})
dfs(0, 0)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | class Solution {
private List<int[]>[] g;
private Map<Integer, Integer> cnt = new HashMap<>();
private long ans;
public long countPalindromePaths(List<Integer> parent, String s) {
int n = parent.size();
g = new List[n];
cnt.put(0, 1);
Arrays.setAll(g, k -> new ArrayList<>());
for (int i = 1; i < n; ++i) {
int p = parent.get(i);
g[p].add(new int[] {i, 1 << (s.charAt(i) - 'a')});
}
dfs(0, 0);
return ans;
}
private void dfs(int i, int xor) {
for (int[] e : g[i]) {
int j = e[0], v = e[1];
int x = xor ^ v;
ans += cnt.getOrDefault(x, 0);
for (int k = 0; k < 26; ++k) {
ans += cnt.getOrDefault(x ^ (1 << k), 0);
}
cnt.merge(x, 1, Integer::sum);
dfs(j, x);
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
public:
long long countPalindromePaths(vector<int>& parent, string s) {
int n = parent.size();
vector<vector<pair<int, int>>> g(n);
unordered_map<int, int> cnt;
cnt[0] = 1;
for (int i = 1; i < n; ++i) {
int p = parent[i];
g[p].emplace_back(i, 1 << (s[i] - 'a'));
}
long long ans = 0;
function<void(int, int)> dfs = [&](int i, int xo) {
for (auto [j, v] : g[i]) {
int x = xo ^ v;
ans += cnt[x];
for (int k = 0; k < 26; ++k) {
ans += cnt[x ^ (1 << k)];
}
++cnt[x];
dfs(j, x);
}
};
dfs(0, 0);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | func countPalindromePaths(parent []int, s string) (ans int64) {
type pair struct{ i, v int }
n := len(parent)
g := make([][]pair, n)
for i := 1; i < n; i++ {
p := parent[i]
g[p] = append(g[p], pair{i, 1 << (s[i] - 'a')})
}
cnt := map[int]int{0: 1}
var dfs func(i, xor int)
dfs = func(i, xor int) {
for _, e := range g[i] {
x := xor ^ e.v
ans += int64(cnt[x])
for k := 0; k < 26; k++ {
ans += int64(cnt[x^(1<<k)])
}
cnt[x]++
dfs(e.i, x)
}
}
dfs(0, 0)
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | function countPalindromePaths(parent: number[], s: string): number {
const n = parent.length;
const g: [number, number][][] = Array.from({ length: n }, () => []);
for (let i = 1; i < n; ++i) {
g[parent[i]].push([i, 1 << (s.charCodeAt(i) - 97)]);
}
const cnt: Map<number, number> = new Map();
cnt.set(0, 1);
let ans = 0;
const dfs = (i: number, xor: number): void => {
for (const [j, v] of g[i]) {
const x = xor ^ v;
ans += cnt.get(x) || 0;
for (let k = 0; k < 26; ++k) {
ans += cnt.get(x ^ (1 << k)) || 0;
}
cnt.set(x, (cnt.get(x) || 0) + 1);
dfs(j, x);
}
};
dfs(0, 0);
return ans;
}
|



