跳转至

277. 搜寻名人 🔒

题目描述

假设你是一个专业的狗仔，参加了一个 n 人派对，其中每个人被从 0 到 n - 1 标号。在这个派对人群当中可能存在一位 “名人”。所谓 “名人” 的定义是：其他所有 n - 1 个人都认识他/她，而他/她并不认识其他任何人。

现在你想要确认这个 “名人” 是谁，或者确定这里没有 “名人”。而你唯一能做的就是问诸如 “A 你好呀，请问你认不认识 B呀？” 的问题，以确定 A 是否认识 B。你需要在（渐近意义上）尽可能少的问题内来确定这位 “名人” 是谁（或者确定这里没有 “名人”）。

在本题中，你可以使用辅助函数 bool knows(a, b) 获取到 A 是否认识 B。请你来实现一个函数 int findCelebrity(n)。

派对最多只会有一个 “名人” 参加。若 “名人” 存在，请返回他/她的编号；若 “名人” 不存在，请返回 -1。

 

示例 1:

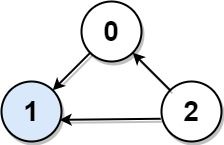
输入: graph = [[1,1,0],[0,1,0],[1,1,1]]
输出: 1
解释: 有编号分别为 0、1 和 2 的三个人。graph[i][j] = 1 代表编号为 i 的人认识编号为 j 的人，而 graph[i][j] = 0 则代表编号为 i 的人不认识编号为 j 的人。“名人” 是编号 1 的人，因为 0 和 2 均认识他/她，但 1 不认识任何人。

示例 2:

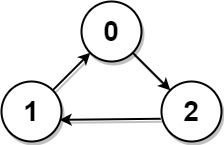
输入: graph = [[1,0,1],[1,1,0],[0,1,1]]
输出: -1
解释: 没有 “名人”

 

提示：

  • n == graph.length == graph[i].length
  • 2 <= n <= 100
  • graph[i][j] 是 0 或 1
  • graph[i][i] == 1

 

进阶：如果允许调用 API knows 的最大次数为 3 * n ，你可以设计一个不超过最大调用次数的解决方案吗？

解法

方法一：O(n) 遍历

经过验证，若暴力遍历，调用 $O(n^2)$ 次 $knows$ 方法，会报 TLE 错误。因此，我们需要寻找更优的解法。

要找出 $n$ 个人中的名人，题目给我们的关键信息是：1. 名人不认识其他所有人；2. 其他所有人都认识名人。

那么，我们初始时假定名人 $ans=0$。然后在 $[1,n)$ 范围内遍历 $i$，若 $ans$ 认识 $i$，说明 $ans$ 不是我们要找的名人，此时我们可以直接将 $ans$ 更新为 $i$。

为什么呢？我们来举个实际的例子。

ans = 0
for i in [1,n) {
    if (ans knows i) {
        ans = i
    }
}

ans = 0

ans not knows 1
ans not knows 2
ans knows 3
ans = 3

ans not knows 4
ans not knows 5
ans not knows 6
ans = 6

这里 $ans$ 认识 $3$，说明 $ans$ 不是名人（即 $0$ 不是名人），那么名人会是 $1$ 或者 $2$ 吗？不会！因为若 $1$ 或者 $2$ 是名人，那么 $0$ 应该认识 $1$ 或者 $2$ 才对，与前面的例子冲突。因此，我们可以直接将 $ans$ 更新为 $i$。

我们找出 $ans$ 之后，接下来再遍历一遍，判断 $ans$ 是否满足名人的条件。若不满足，返回 $-1$。

否则遍历结束，返回 $ans$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
# The knows API is already defined for you.
# return a bool, whether a knows b
# def knows(a: int, b: int) -> bool:


class Solution:
    def findCelebrity(self, n: int) -> int:
        ans = 0
        for i in range(1, n):
            if knows(ans, i):
                ans = i
        for i in range(n):
            if ans != i:
                if knows(ans, i) or not knows(i, ans):
                    return -1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
/* The knows API is defined in the parent class Relation.
      boolean knows(int a, int b); */

public class Solution extends Relation {
    public int findCelebrity(int n) {
        int ans = 0;
        for (int i = 1; i < n; ++i) {
            if (knows(ans, i)) {
                ans = i;
            }
        }
        for (int i = 0; i < n; ++i) {
            if (ans != i) {
                if (knows(ans, i) || !knows(i, ans)) {
                    return -1;
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
/* The knows API is defined for you.
      bool knows(int a, int b); */

class Solution {
public:
    int findCelebrity(int n) {
        int ans = 0;
        for (int i = 1; i < n; ++i) {
            if (knows(ans, i)) {
                ans = i;
            }
        }
        for (int i = 0; i < n; ++i) {
            if (ans != i) {
                if (knows(ans, i) || !knows(i, ans)) {
                    return -1;
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * The knows API is already defined for you.
 *     knows := func(a int, b int) bool
 */
func solution(knows func(a int, b int) bool) func(n int) int {
    return func(n int) int {
        ans := 0
        for i := 1; i < n; i++ {
            if knows(ans, i) {
                ans = i
            }
        }
        for i := 0; i < n; i++ {
            if ans != i {
                if knows(ans, i) || !knows(i, ans) {
                    return -1
                }
            }
        }
        return ans
    }
}

评论