
题目描述
给定一个以 0 为起始索引的整数 二维数组 nodes ,你的任务是确定给定的数组是否表示某个 二叉 树的 前序 遍历。
对于每个索引 i ,nodes[i] = [id, parentId] ,其中 id 是索引 i 处节点的 id,parentId 是其在树中的父节点 id(如果该节点没有父节点,则 parentId = -1 )。
如果给定的数组表示某个树的前序遍历,则返回 true ,否则返回 false 。
注意:树的 前序 遍历是一种递归的遍历方式,它首先访问当前节点,然后对左子节点进行前序遍历,最后对右子节点进行前序遍历。
示例 1:
输入:nodes = [[0,-1],[1,0],[2,0],[3,2],[4,2]]
输出:true
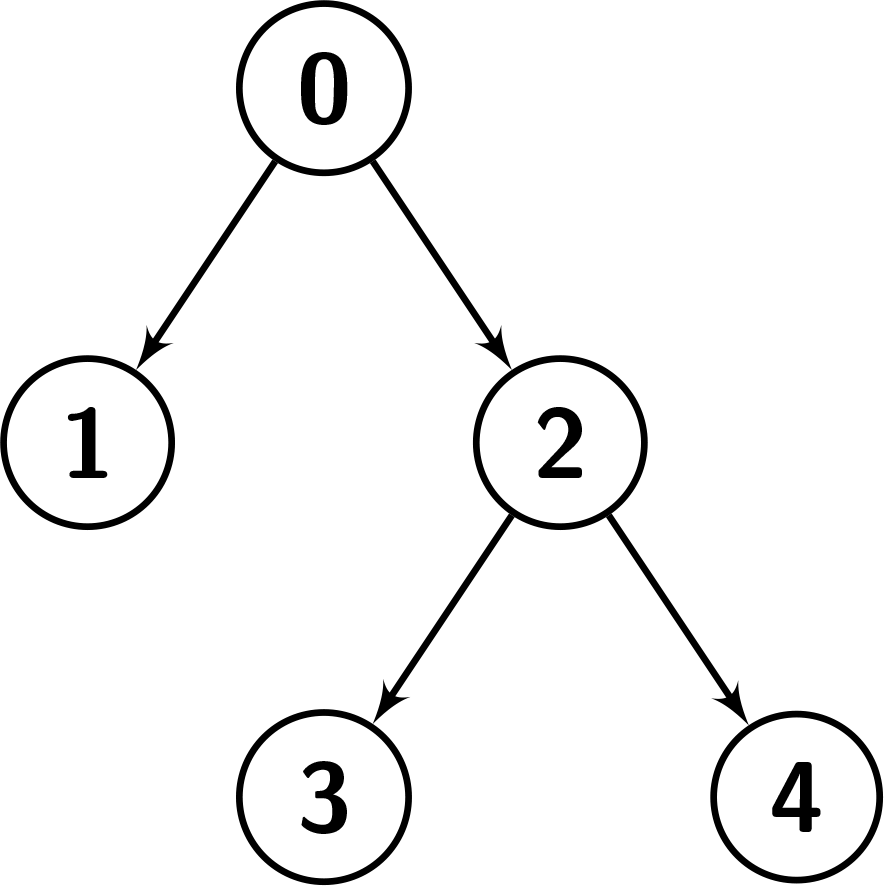
解释:给定的 nodes 数组可以构成下面图片中的树。
我们可以验证这是树的前序遍历,首先访问节点 0,然后对左子节点进行前序遍历,即 [1] ,然后对右子节点进行前序遍历,即 [2,3,4] 。
示例 2:
输入:nodes = [[0,-1],[1,0],[2,0],[3,1],[4,1]]
输出:false
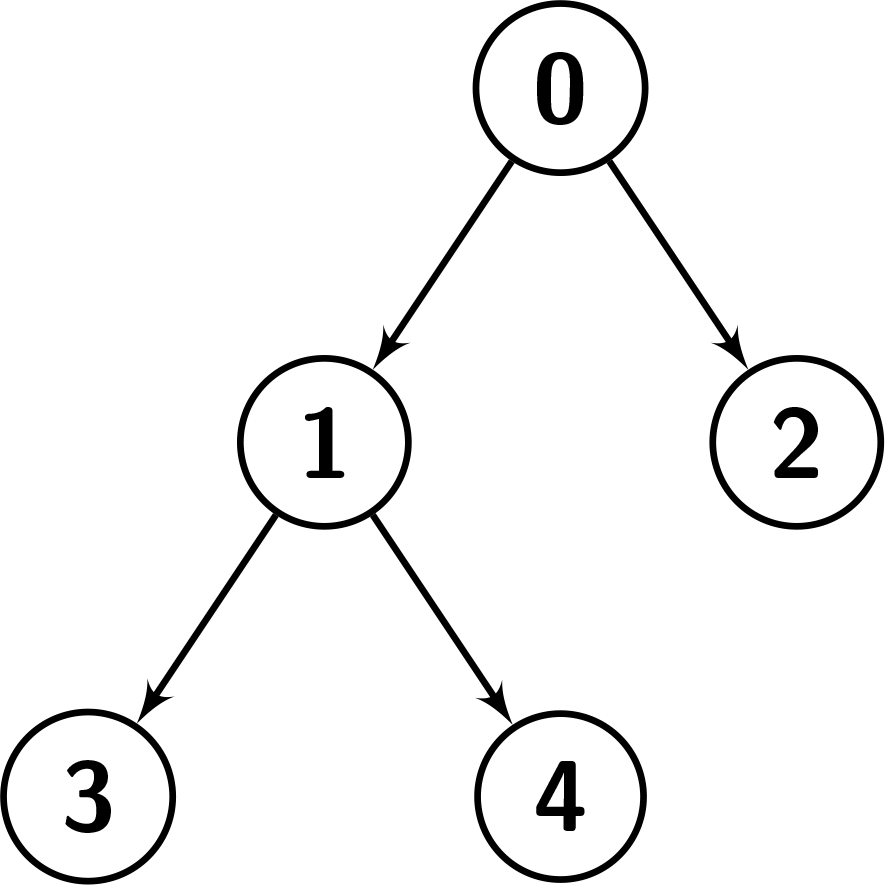
解释:给定的 nodes 数组可以构成下面图片中的树。
对于前序遍历,首先访问节点 0,然后对左子节点进行前序遍历,即 [1,3,4],但是我们可以看到在给定的顺序中,2 位于 1 和 3 之间,因此它不是树的前序遍历。
提示:
1 <= nodes.length <= 105nodes[i].length == 20 <= nodes[i][0] <= 105-1 <= nodes[i][1] <= 105- 生成的输入保证
nodes 可以组成二叉树。
解法
方法一:DFS
我们先根据 \(nodes\) 数据构建图 \(g\),其中 \(g[i]\) 表示节点 \(i\) 的所有子节点。
接下来,设计一个函数 \(dfs(i)\),表示从节点 \(i\) 开始进行先序遍历,用一个变量 \(k\) 表示当前遍历到 \(nodes\) 列表的第 \(k\) 个节点,初始时 \(k=0\)。
函数 \(dfs(i)\) 的执行逻辑如下:
- 如果 \(i \neq nodes[k][0]\),说明当前序列不是二叉树的先序遍历序列,返回
false。
- 否则,我们将 \(k\) 加 \(1\),然后递归搜索 \(i\) 的所有子节点,如果搜索过程中发现
false,那么提前返回 false,否则搜索结束,返回 true。
在主函数中,我们调用 \(dfs(nodes[0][0])\),如果返回值为 true,并且 \(k = |nodes|\),那么 \(nodes\) 序列是二叉树的先序遍历序列,返回 true,否则返回 false。
时间复杂度 \(O(n)\),空间复杂度 \(O(n)\)。其中 \(n\) 是 \(nodes\) 中的节点数目。
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | class Solution:
def isPreorder(self, nodes: List[List[int]]) -> bool:
def dfs(i: int) -> int:
nonlocal k
if i != nodes[k][0]:
return False
k += 1
return all(dfs(j) for j in g[i])
g = defaultdict(list)
for i, p in nodes:
g[p].append(i)
k = 0
return dfs(nodes[0][0]) and k == len(nodes)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | class Solution {
private Map<Integer, List<Integer>> g = new HashMap<>();
private List<List<Integer>> nodes;
private int k;
public boolean isPreorder(List<List<Integer>> nodes) {
this.nodes = nodes;
for (var node : nodes) {
g.computeIfAbsent(node.get(1), key -> new ArrayList<>()).add(node.get(0));
}
return dfs(nodes.get(0).get(0)) && k == nodes.size();
}
private boolean dfs(int i) {
if (i != nodes.get(k).get(0)) {
return false;
}
++k;
for (int j : g.getOrDefault(i, List.of())) {
if (!dfs(j)) {
return false;
}
}
return true;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution {
public:
bool isPreorder(vector<vector<int>>& nodes) {
int k = 0;
unordered_map<int, vector<int>> g;
for (auto& node : nodes) {
g[node[1]].push_back(node[0]);
}
function<bool(int)> dfs = [&](int i) {
if (i != nodes[k][0]) {
return false;
}
++k;
for (int j : g[i]) {
if (!dfs(j)) {
return false;
}
}
return true;
};
return dfs(nodes[0][0]) && k == nodes.size();
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | func isPreorder(nodes [][]int) bool {
k := 0
g := map[int][]int{}
for _, node := range nodes {
g[node[1]] = append(g[node[1]], node[0])
}
var dfs func(int) bool
dfs = func(i int) bool {
if i != nodes[k][0] {
return false
}
k++
for _, j := range g[i] {
if !dfs(j) {
return false
}
}
return true
}
return dfs(nodes[0][0]) && k == len(nodes)
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | function isPreorder(nodes: number[][]): boolean {
let k = 0;
const g: Map<number, number[]> = new Map();
for (const [i, p] of nodes) {
if (!g.has(p)) {
g.set(p, []);
}
g.get(p)!.push(i);
}
const dfs = (i: number): boolean => {
if (i !== nodes[k][0]) {
return false;
}
++k;
for (const j of g.get(i) ?? []) {
if (!dfs(j)) {
return false;
}
}
return true;
};
return dfs(nodes[0][0]) && k === nodes.length;
}
|


