


题目描述
给你一个整数 n 和一个下标从 0 开始的 二维数组 queries ,其中 queries[i] = [typei, indexi, vali] 。
一开始,给你一个下标从 0 开始的 n x n 矩阵,所有元素均为 0 。每一个查询,你需要执行以下操作之一:
- 如果
typei == 0 ,将第 indexi 行的元素全部修改为 vali ,覆盖任何之前的值。
- 如果
typei == 1 ,将第 indexi 列的元素全部修改为 vali ,覆盖任何之前的值。
请你执行完所有查询以后,返回矩阵中所有整数的和。
示例 1:
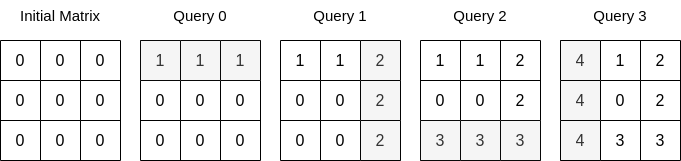
输入:n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
输出:23
解释:上图展示了每个查询以后矩阵的值。所有操作执行完以后,矩阵元素之和为 23 。
示例 2:
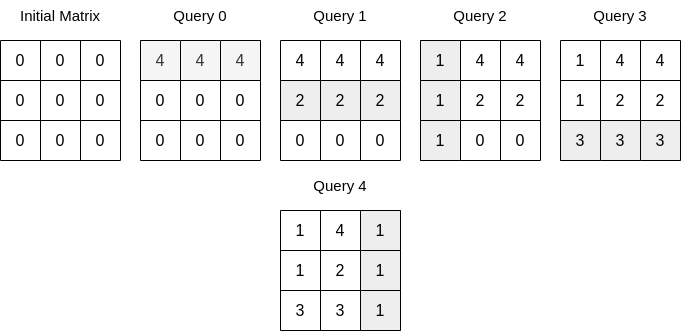
输入:n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
输出:17
解释:上图展示了每一个查询操作之后的矩阵。所有操作执行完以后,矩阵元素之和为 17 。
提示:
1 <= n <= 1041 <= queries.length <= 5 * 104queries[i].length == 30 <= typei <= 10 <= indexi < n0 <= vali <= 105
解法
方法一:哈希表
由于每一行、每一列的值取决于最后一次的修改,因此,我们不妨倒序遍历所有的查询,使用哈希表 \(row\) 和 \(col\) 记录有哪些行和列被修改过。
对于每一次查询 \((t, i, v)\):
- 如果 \(t = 0\),那么我们判断第 \(i\) 行是否被修改过,如果没有,那么我们将 \(v \times (n - |col|)\) 累加到答案中,其中 \(|col|\) 表示 \(col\) 的大小,然后将 \(i\) 加入 \(row\) 中;
- 如果 \(t = 1\),那么我们判断第 \(i\) 列是否被修改过,如果没有,那么我们将 \(v \times (n - |row|)\) 累加到答案中,其中 \(|row|\) 表示 \(row\) 的大小,然后将 \(i\) 加入 \(col\) 中。
最后返回答案。
时间复杂度 \(O(m)\),空间复杂度 \(O(n)\)。其中 \(m\) 表示查询的次数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | class Solution:
def matrixSumQueries(self, n: int, queries: List[List[int]]) -> int:
row = set()
col = set()
ans = 0
for t, i, v in queries[::-1]:
if t == 0:
if i not in row:
ans += v * (n - len(col))
row.add(i)
else:
if i not in col:
ans += v * (n - len(row))
col.add(i)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | class Solution {
public long matrixSumQueries(int n, int[][] queries) {
Set<Integer> row = new HashSet<>();
Set<Integer> col = new HashSet<>();
int m = queries.length;
long ans = 0;
for (int k = m - 1; k >= 0; --k) {
var q = queries[k];
int t = q[0], i = q[1], v = q[2];
if (t == 0) {
if (row.add(i)) {
ans += 1L * (n - col.size()) * v;
}
} else {
if (col.add(i)) {
ans += 1L * (n - row.size()) * v;
}
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution {
public:
long long matrixSumQueries(int n, vector<vector<int>>& queries) {
unordered_set<int> row, col;
reverse(queries.begin(), queries.end());
long long ans = 0;
for (auto& q : queries) {
int t = q[0], i = q[1], v = q[2];
if (t == 0) {
if (!row.count(i)) {
ans += 1LL * (n - col.size()) * v;
row.insert(i);
}
} else {
if (!col.count(i)) {
ans += 1LL * (n - row.size()) * v;
col.insert(i);
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | func matrixSumQueries(n int, queries [][]int) (ans int64) {
row, col := map[int]bool{}, map[int]bool{}
m := len(queries)
for k := m - 1; k >= 0; k-- {
t, i, v := queries[k][0], queries[k][1], queries[k][2]
if t == 0 {
if !row[i] {
ans += int64(v * (n - len(col)))
row[i] = true
}
} else {
if !col[i] {
ans += int64(v * (n - len(row)))
col[i] = true
}
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | function matrixSumQueries(n: number, queries: number[][]): number {
const row: Set<number> = new Set();
const col: Set<number> = new Set();
let ans = 0;
queries.reverse();
for (const [t, i, v] of queries) {
if (t === 0) {
if (!row.has(i)) {
ans += v * (n - col.size);
row.add(i);
}
} else {
if (!col.has(i)) {
ans += v * (n - row.size);
col.add(i);
}
}
}
return ans;
}
|




