


题目描述
给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat,你可以选择任一单元格作为 起始单元格 。
从起始单元格出发,你可以移动到 同一行或同一列 中的任何其他单元格,但前提是目标单元格的值 严格大于 当前单元格的值。
你可以多次重复这一过程,从一个单元格移动到另一个单元格,直到无法再进行任何移动。
请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。
返回一个表示可访问单元格最大数量的整数。
示例 1:
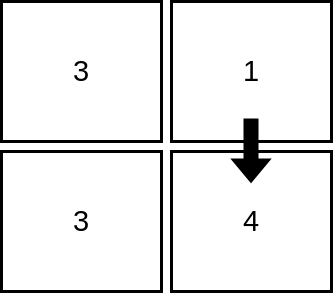
输入:mat = [[3,1],[3,4]]
输出:2
解释:上图展示了从第 1 行、第 2 列的单元格开始,可以访问 2 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 2 个单元格,因此答案是 2 。
示例 2:
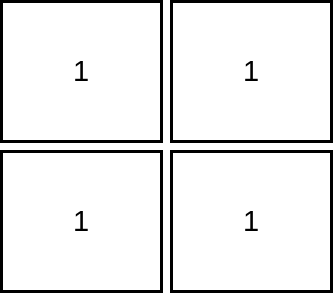
输入:mat = [[1,1],[1,1]]
输出:1
解释:由于目标单元格必须严格大于当前单元格,在本示例中只能访问 1 个单元格。
示例 3:
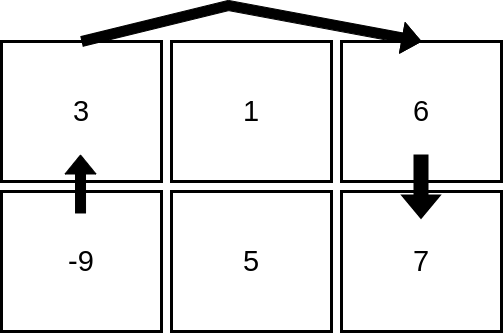
输入:mat = [[3,1,6],[-9,5,7]]
输出:4
解释:上图展示了从第 2 行、第 1 列的单元格开始,可以访问 4 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 4 个单元格,因此答案是 4 。
提示:
m == mat.length n == mat[i].length 1 <= m, n <= 1051 <= m * n <= 105-105 <= mat[i][j] <= 105
解法
方法一:排序 + 动态规划
根据题目描述,我们顺序移动的单元格的值必须严格递增,因此,我们不妨用一个哈希表 \(g\) 来记录每个值对应的所有单元格的位置,然后按照值的大小从小到大遍历。
在这个过程中,我们可以维护两个数组 rowMax 和 colMax,分别记录每一行和每一列的最大递增长度。初始时,这两个数组的所有元素都为 \(0\)。
对于每个值对应的所有单元格位置,我们按照位置顺序遍历,对于每个位置 \((i, j)\),我们可以计算出以该位置为终点的最大递增长度为 \(1 + \max(\textit{rowMax}[i], \textit{colMax}[j])\),更新答案,然后更新 rowMax[i] 和 colMax[j]。
最后返回答案即可。
时间复杂度 \(O(m \times n \times \log(m \times n))\),空间复杂度 \(O(m \times n)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | class Solution:
def maxIncreasingCells(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0])
g = defaultdict(list)
for i in range(m):
for j in range(n):
g[mat[i][j]].append((i, j))
rowMax = [0] * m
colMax = [0] * n
ans = 0
for _, pos in sorted(g.items()):
mx = []
for i, j in pos:
mx.append(1 + max(rowMax[i], colMax[j]))
ans = max(ans, mx[-1])
for k, (i, j) in enumerate(pos):
rowMax[i] = max(rowMax[i], mx[k])
colMax[j] = max(colMax[j], mx[k])
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | class Solution {
public int maxIncreasingCells(int[][] mat) {
int m = mat.length, n = mat[0].length;
TreeMap<Integer, List<int[]>> g = new TreeMap<>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
g.computeIfAbsent(mat[i][j], k -> new ArrayList<>()).add(new int[] {i, j});
}
}
int[] rowMax = new int[m];
int[] colMax = new int[n];
int ans = 0;
for (var e : g.entrySet()) {
var pos = e.getValue();
int[] mx = new int[pos.size()];
int k = 0;
for (var p : pos) {
int i = p[0], j = p[1];
mx[k] = Math.max(rowMax[i], colMax[j]) + 1;
ans = Math.max(ans, mx[k++]);
}
for (k = 0; k < mx.length; ++k) {
int i = pos.get(k)[0], j = pos.get(k)[1];
rowMax[i] = Math.max(rowMax[i], mx[k]);
colMax[j] = Math.max(colMax[j], mx[k]);
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | class Solution {
public:
int maxIncreasingCells(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
map<int, vector<pair<int, int>>> g;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
g[mat[i][j]].emplace_back(i, j);
}
}
vector<int> rowMax(m);
vector<int> colMax(n);
int ans = 0;
for (auto& [_, pos] : g) {
vector<int> mx;
for (auto& [i, j] : pos) {
mx.push_back(max(rowMax[i], colMax[j]) + 1);
ans = max(ans, mx.back());
}
for (int k = 0; k < mx.size(); ++k) {
auto& [i, j] = pos[k];
rowMax[i] = max(rowMax[i], mx[k]);
colMax[j] = max(colMax[j], mx[k]);
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | func maxIncreasingCells(mat [][]int) (ans int) {
m, n := len(mat), len(mat[0])
g := map[int][][2]int{}
for i, row := range mat {
for j, v := range row {
g[v] = append(g[v], [2]int{i, j})
}
}
nums := make([]int, 0, len(g))
for k := range g {
nums = append(nums, k)
}
sort.Ints(nums)
rowMax := make([]int, m)
colMax := make([]int, n)
for _, k := range nums {
pos := g[k]
mx := make([]int, len(pos))
for i, p := range pos {
mx[i] = max(rowMax[p[0]], colMax[p[1]]) + 1
ans = max(ans, mx[i])
}
for i, p := range pos {
rowMax[p[0]] = max(rowMax[p[0]], mx[i])
colMax[p[1]] = max(colMax[p[1]], mx[i])
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | function maxIncreasingCells(mat: number[][]): number {
const m = mat.length;
const n = mat[0].length;
const g: { [key: number]: [number, number][] } = {};
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (!g[mat[i][j]]) {
g[mat[i][j]] = [];
}
g[mat[i][j]].push([i, j]);
}
}
const rowMax = Array(m).fill(0);
const colMax = Array(n).fill(0);
let ans = 0;
const sortedKeys = Object.keys(g)
.map(Number)
.sort((a, b) => a - b);
for (const key of sortedKeys) {
const pos = g[key];
const mx: number[] = [];
for (const [i, j] of pos) {
mx.push(1 + Math.max(rowMax[i], colMax[j]));
ans = Math.max(ans, mx[mx.length - 1]);
}
for (let k = 0; k < pos.length; k++) {
const [i, j] = pos[k];
rowMax[i] = Math.max(rowMax[i], mx[k]);
colMax[j] = Math.max(colMax[j], mx[k]);
}
}
return ans;
}
|





