


题目描述
给你一个 n 个节点的 无向带权连通 图,节点编号为 0 到 n - 1 ,再给你一个整数数组 edges ,其中 edges[i] = [ai, bi, wi] 表示节点 ai 和 bi 之间有一条边权为 wi 的边。
部分边的边权为 -1(wi = -1),其他边的边权都为 正 数(wi > 0)。
你需要将所有边权为 -1 的边都修改为范围 [1, 2 * 109] 中的 正整数 ,使得从节点 source 到节点 destination 的 最短距离 为整数 target 。如果有 多种 修改方案可以使 source 和 destination 之间的最短距离等于 target ,你可以返回任意一种方案。
如果存在使 source 到 destination 最短距离为 target 的方案,请你按任意顺序返回包含所有边的数组(包括未修改边权的边)。如果不存在这样的方案,请你返回一个 空数组 。
注意:你不能修改一开始边权为正数的边。
示例 1:
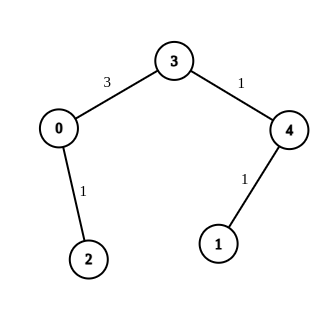
输入:n = 5, edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5
输出:[[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
解释:上图展示了一个满足题意的修改方案,从 0 到 1 的最短距离为 5 。
示例 2:
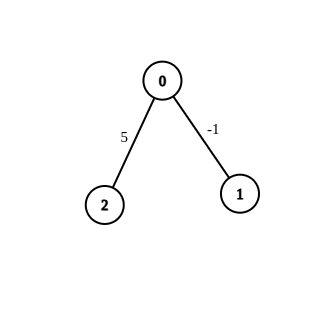
输入:n = 3, edges = [[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6
输出:[]
解释:上图是一开始的图。没有办法通过修改边权为 -1 的边,使得 0 到 2 的最短距离等于 6 ,所以返回一个空数组。
示例 3:
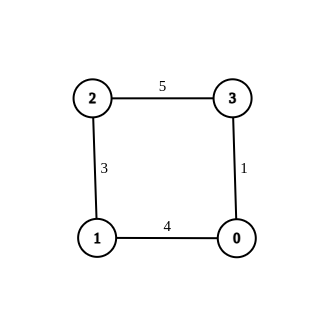
输入:n = 4, edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6
输出:[[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
解释:上图展示了一个满足题意的修改方案,从 0 到 2 的最短距离为 6 。
提示:
1 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= ai, bi < nwi = -1 或者 1 <= wi <= 107ai != bi0 <= source, destination < nsource != destination1 <= target <= 109- 输入的图是连通图,且没有自环和重边。
解法
方法一:最短路(Dijkstra 算法)
我们先不考虑边权为 \(-1\) 的边,使用 Dijkstra 算法求出从 \(source\) 到 \(destination\) 的最短距离 \(d\)。
如果 \(d \lt target\),说明存在一条完全由正权边组成的最短路径,此时无论我们如何修改边权为 \(-1\) 的边,都无法使得 \(source\) 到 \(destination\) 的最短距离等于 \(target\),因此不存在满足题意的修改方案,返回一个空数组即可。
如果 \(d = target\),说明存在一条完全由正权边组成的、长度为 \(target\) 的最短路径,此时我们可以将所有边权为 \(-1\) 的边修改为最大值 \(2 \times 10^9\) 即可。
如果 \(d \gt target\),我们可以尝试往图中加入一条边权为 \(-1\) 的边,将边权设置为 \(1\),然后再次使用 Dijkstra 算法求出从 \(source\) 到 \(destination\) 的最短距离 \(d\)。
- 如果最短距离 \(d \leq target\),说明加入这条边后,可以使得最短路变短,而且最短路也一定经过这条边,那么我们只需要将这条边的边权改为 \(target-d+1\),就可以使得最短路等于 \(target\)。然后我们将其余的边权为 \(-1\) 的边修改为最大值 \(2 \times 10^9\) 即可。
- 如果最短距离 \(d \gt target\),说明加入这条边后,最短路不会变短,那么我们贪心地将这条边的边权保持为 \(-1\),然后继续尝试加入其余的边权为 \(-1\) 的边。
时间复杂度 \(O(n^3)\),空间复杂度 \(O(n^2)\)。其中 \(n\) 是图中的点数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | class Solution:
def modifiedGraphEdges(
self, n: int, edges: List[List[int]], source: int, destination: int, target: int
) -> List[List[int]]:
def dijkstra(edges: List[List[int]]) -> int:
g = [[inf] * n for _ in range(n)]
for a, b, w in edges:
if w == -1:
continue
g[a][b] = g[b][a] = w
dist = [inf] * n
dist[source] = 0
vis = [False] * n
for _ in range(n):
k = -1
for j in range(n):
if not vis[j] and (k == -1 or dist[k] > dist[j]):
k = j
vis[k] = True
for j in range(n):
dist[j] = min(dist[j], dist[k] + g[k][j])
return dist[destination]
inf = 2 * 10**9
d = dijkstra(edges)
if d < target:
return []
ok = d == target
for e in edges:
if e[2] > 0:
continue
if ok:
e[2] = inf
continue
e[2] = 1
d = dijkstra(edges)
if d <= target:
ok = True
e[2] += target - d
return edges if ok else []
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60 | class Solution {
private final int inf = 2000000000;
public int[][] modifiedGraphEdges(
int n, int[][] edges, int source, int destination, int target) {
long d = dijkstra(edges, n, source, destination);
if (d < target) {
return new int[0][];
}
boolean ok = d == target;
for (var e : edges) {
if (e[2] > 0) {
continue;
}
if (ok) {
e[2] = inf;
continue;
}
e[2] = 1;
d = dijkstra(edges, n, source, destination);
if (d <= target) {
ok = true;
e[2] += target - d;
}
}
return ok ? edges : new int[0][];
}
private long dijkstra(int[][] edges, int n, int src, int dest) {
int[][] g = new int[n][n];
long[] dist = new long[n];
Arrays.fill(dist, inf);
dist[src] = 0;
for (var f : g) {
Arrays.fill(f, inf);
}
for (var e : edges) {
int a = e[0], b = e[1], w = e[2];
if (w == -1) {
continue;
}
g[a][b] = w;
g[b][a] = w;
}
boolean[] vis = new boolean[n];
for (int i = 0; i < n; ++i) {
int k = -1;
for (int j = 0; j < n; ++j) {
if (!vis[j] && (k == -1 || dist[k] > dist[j])) {
k = j;
}
}
vis[k] = true;
for (int j = 0; j < n; ++j) {
dist[j] = Math.min(dist[j], dist[k] + g[k][j]);
}
}
return dist[dest];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62 | using ll = long long;
const int inf = 2e9;
class Solution {
public:
vector<vector<int>> modifiedGraphEdges(int n, vector<vector<int>>& edges, int source, int destination, int target) {
ll d = dijkstra(edges, n, source, destination);
if (d < target) {
return {};
}
bool ok = d == target;
for (auto& e : edges) {
if (e[2] > 0) {
continue;
}
if (ok) {
e[2] = inf;
continue;
}
e[2] = 1;
d = dijkstra(edges, n, source, destination);
if (d <= target) {
ok = true;
e[2] += target - d;
}
}
return ok ? edges : vector<vector<int>>{};
}
ll dijkstra(vector<vector<int>>& edges, int n, int src, int dest) {
ll g[n][n];
ll dist[n];
bool vis[n];
for (int i = 0; i < n; ++i) {
fill(g[i], g[i] + n, inf);
dist[i] = inf;
vis[i] = false;
}
dist[src] = 0;
for (auto& e : edges) {
int a = e[0], b = e[1], w = e[2];
if (w == -1) {
continue;
}
g[a][b] = w;
g[b][a] = w;
}
for (int i = 0; i < n; ++i) {
int k = -1;
for (int j = 0; j < n; ++j) {
if (!vis[j] && (k == -1 || dist[j] < dist[k])) {
k = j;
}
}
vis[k] = true;
for (int j = 0; j < n; ++j) {
dist[j] = min(dist[j], dist[k] + g[k][j]);
}
}
return dist[dest];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60 | func modifiedGraphEdges(n int, edges [][]int, source int, destination int, target int) [][]int {
const inf int = 2e9
dijkstra := func(edges [][]int) int {
g := make([][]int, n)
dist := make([]int, n)
vis := make([]bool, n)
for i := range g {
g[i] = make([]int, n)
for j := range g[i] {
g[i][j] = inf
}
dist[i] = inf
}
dist[source] = 0
for _, e := range edges {
a, b, w := e[0], e[1], e[2]
if w == -1 {
continue
}
g[a][b], g[b][a] = w, w
}
for i := 0; i < n; i++ {
k := -1
for j := 0; j < n; j++ {
if !vis[j] && (k == -1 || dist[j] < dist[k]) {
k = j
}
}
vis[k] = true
for j := 0; j < n; j++ {
dist[j] = min(dist[j], dist[k]+g[k][j])
}
}
return dist[destination]
}
d := dijkstra(edges)
if d < target {
return [][]int{}
}
ok := d == target
for _, e := range edges {
if e[2] > 0 {
continue
}
if ok {
e[2] = inf
continue
}
e[2] = 1
d := dijkstra(edges)
if d <= target {
ok = true
e[2] += target - d
}
}
if ok {
return edges
}
return [][]int{}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58 | function modifiedGraphEdges(
n: number,
edges: number[][],
source: number,
destination: number,
target: number,
): number[][] {
const inf = 2e9;
const dijkstra = (edges: number[][]): number => {
const g: number[][] = Array(n)
.fill(0)
.map(() => Array(n).fill(inf));
const dist: number[] = Array(n).fill(inf);
const vis: boolean[] = Array(n).fill(false);
for (const [a, b, w] of edges) {
if (w === -1) {
continue;
}
g[a][b] = w;
g[b][a] = w;
}
dist[source] = 0;
for (let i = 0; i < n; ++i) {
let k = -1;
for (let j = 0; j < n; ++j) {
if (!vis[j] && (k === -1 || dist[j] < dist[k])) {
k = j;
}
}
vis[k] = true;
for (let j = 0; j < n; ++j) {
dist[j] = Math.min(dist[j], dist[k] + g[k][j]);
}
}
return dist[destination];
};
let d = dijkstra(edges);
if (d < target) {
return [];
}
let ok = d === target;
for (const e of edges) {
if (e[2] > 0) {
continue;
}
if (ok) {
e[2] = inf;
continue;
}
e[2] = 1;
d = dijkstra(edges);
if (d <= target) {
ok = true;
e[2] += target - d;
}
}
return ok ? edges : [];
}
|





