


题目描述
给你一个整数 n 。现有一个包含 n 个顶点的 无向 图,顶点按从 0 到 n - 1 编号。给你一个二维整数数组 edges 其中 edges[i] = [ai, bi] 表示顶点 ai 和 bi 之间存在一条 无向 边。
返回图中 完全连通分量 的数量。
如果在子图中任意两个顶点之间都存在路径,并且子图中没有任何一个顶点与子图外部的顶点共享边,则称其为 连通分量 。
如果连通分量中每对节点之间都存在一条边,则称其为 完全连通分量 。
示例 1:
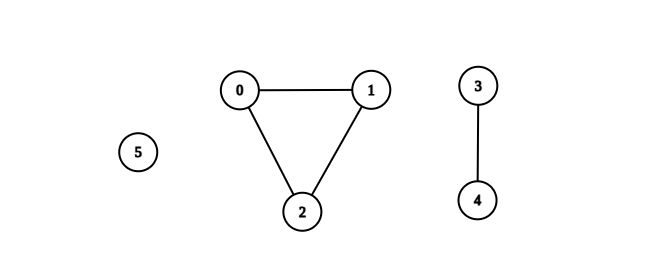
输入:n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
输出:3
解释:如上图所示,可以看到此图所有分量都是完全连通分量。
示例 2:
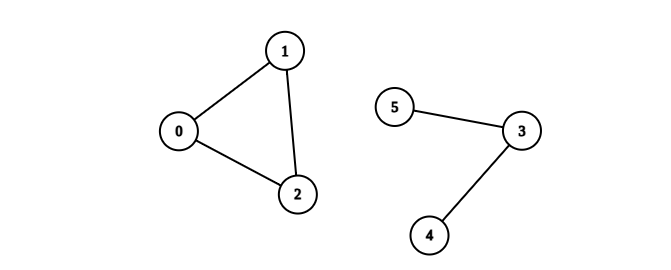
输入:n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
输出:1
解释:包含节点 0、1 和 2 的分量是完全连通分量,因为每对节点之间都存在一条边。
包含节点 3 、4 和 5 的分量不是完全连通分量,因为节点 4 和 5 之间不存在边。
因此,在图中完全连接分量的数量是 1 。
提示:
1 <= n <= 500 <= edges.length <= n * (n - 1) / 2edges[i].length == 20 <= ai, bi <= n - 1ai != bi- 不存在重复的边
解法
方法一:DFS
我们先根据题目给定的边建立一个邻接表 \(g\),其中 \(g[i]\) 表示顶点 \(i\) 的邻接点集合。
然后我们从 \(0\) 开始遍历所有顶点,如果当前顶点没有被访问过,我们就从当前顶点开始进行深度优先搜索,统计当前连通分量的顶点数 \(x\) 和边数 \(y\)。如果 \(\frac{x(x-1)}{2} = y\),那么当前连通分量就是完全连通分量,我们将答案加一。
最后我们返回答案即可。
时间复杂度 \(O(n + m)\),空间复杂度 \(O(n + m)\)。其中 \(n\) 和 \(m\) 分别是顶点数和边数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution:
def countCompleteComponents(self, n: int, edges: List[List[int]]) -> int:
def dfs(i: int) -> (int, int):
vis[i] = True
x, y = 1, len(g[i])
for j in g[i]:
if not vis[j]:
a, b = dfs(j)
x += a
y += b
return x, y
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
vis = [False] * n
ans = 0
for i in range(n):
if not vis[i]:
a, b = dfs(i)
ans += a * (a - 1) == b
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | class Solution {
private List<Integer>[] g;
private boolean[] vis;
public int countCompleteComponents(int n, int[][] edges) {
g = new List[n];
vis = new boolean[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (int[] e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
if (!vis[i]) {
int[] t = dfs(i);
if (t[0] * (t[0] - 1) == t[1]) {
++ans;
}
}
}
return ans;
}
private int[] dfs(int i) {
vis[i] = true;
int x = 1, y = g[i].size();
for (int j : g[i]) {
if (!vis[j]) {
int[] t = dfs(j);
x += t[0];
y += t[1];
}
}
return new int[] {x, y};
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | class Solution {
public:
int countCompleteComponents(int n, vector<vector<int>>& edges) {
vector<vector<int>> g(n);
bool vis[n];
memset(vis, false, sizeof(vis));
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
function<pair<int, int>(int)> dfs = [&](int i) -> pair<int, int> {
vis[i] = true;
int x = 1, y = g[i].size();
for (int j : g[i]) {
if (!vis[j]) {
auto [a, b] = dfs(j);
x += a;
y += b;
}
}
return make_pair(x, y);
};
int ans = 0;
for (int i = 0; i < n; ++i) {
if (!vis[i]) {
auto [a, b] = dfs(i);
if (a * (a - 1) == b) {
++ans;
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | func countCompleteComponents(n int, edges [][]int) (ans int) {
g := make([][]int, n)
vis := make([]bool, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
var dfs func(int) (int, int)
dfs = func(i int) (int, int) {
vis[i] = true
x, y := 1, len(g[i])
for _, j := range g[i] {
if !vis[j] {
a, b := dfs(j)
x += a
y += b
}
}
return x, y
}
for i := range vis {
if !vis[i] {
a, b := dfs(i)
if a*(a-1) == b {
ans++
}
}
}
return
}
|
方法二:取巧做法
要解决的问题:
- 如何保存每一个节点与其它点联通状态
- 如何判断多个点是否是一个联通图
对于第一点:实际上就是保存了当前到每个点的联通点集合(包括自己),方便后续判等。
第二点:有了第一点之后,如果是连通图中的点就有:
- 此点包含此联通图中所有的点(包括自己)
- 并且只包含此联通图中的点
拿示例一举例:
- 5 包含的联通点有且只有自己,所以是连通图
- 0 包含 0、1、2,同理 1、2 点也是
- 3 和 4 也是包含自己和彼此
- 基于以上就有以下代码实现:




