
题目描述
现给定你一个整数 n 。考虑一个边长为 n 的等边三角形,被分成 n2 个单位等边三角形。这个三角形有 n 个 从 1 开始编号 的行,其中第 i 行有 2i - 1 个单位等边三角形。
第 i 行的三角形也是 从 1 开始编号 的,其坐标从 (i, 1) 到 (i, 2i - 1) 。下面的图像显示了一个边长为 4 的三角形及其三角形的索引。
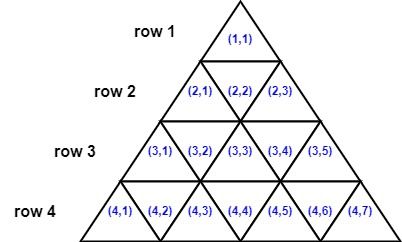
如果两个三角形 共享一条边 ,则它们是 相邻 的。例如:
- 三角形
(1,1) 和 (2,2) 是相邻的。
- 三角形
(3,2) 和 (3,3) 是相邻的。
- 三角形
(2,2) 和 (3,3) 不相邻,因为它们没有共享任何边。
初始时,所有单位三角形都是 白色 的。你想选择 k 个三角形并将它们涂成 红色 。然后我们将运行以下算法:
- 选择一个 至少有两个 红色相邻三角形的白色三角形。
- 将该三角形涂成 红色 。
- 回到步骤 1。
选择最小的 k 并在运行此算法之前将 k 个三角形涂成红色,使得在算法停止后,所有单元三角形都被涂成红色。
返回一个二维列表,其中包含你要最初涂成红色的三角形的坐标。答案必须尽可能小。如果有多个有效的解决方案,请返回其中任意一个。
示例 1 :
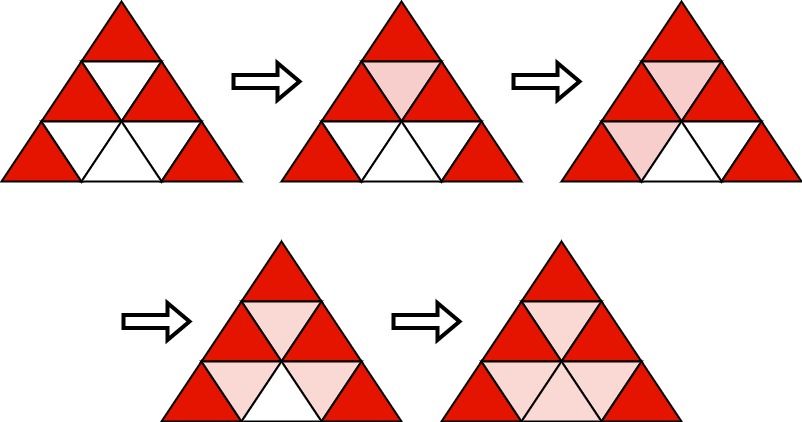
输入:n = 3
输出:[[1,1],[2,1],[2,3],[3,1],[3,5]]
解释:初始时,我们选择展示的5个三角形染成红色。然后,我们运行以下算法:
- 选择(2,2),它有三个红色相邻的三角形,并将其染成红色。
- 选择(3,2),它有两个红色相邻的三角形,并将其染成红色。
- 选择(3,4),它有三个红色相邻的三角形,并将其染成红色。
- 选择(3,3),它有三个红色相邻的三角形,并将其染成红色。
可以证明,选择任何4个三角形并运行算法都无法将所有三角形都染成红色。
示例 2 :
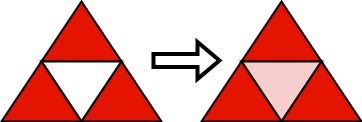
输入:n = 2
输出:[[1,1],[2,1],[2,3]]
解释:初始时,我们选择图中所示的 3 个三角形为红色。然后,我们运行以下算法:
-选择有三个红色相邻的 (2,2) 三角形并将其染成红色。
可以证明,选择任意 2 个三角形并运行该算法都不能使所有三角形变为红色。
提示:
解法
方法一:找规律
我们画图观察,可以发现,第一行只有一个三角形,一定要涂色,而从最后一行开始,到第二行结束,每四行的涂色方案是一样的:
- 最后一行涂色坐标为 \((n, 1)\), \((n, 3)\), ..., \((n, 2n - 1)\)。
- 第 \(n - 1\) 行涂色坐标为 \((n - 1, 2)\)。
- 第 \(n - 2\) 行涂色坐标为 \((n - 2, 3)\), \((n - 2, 5)\), ..., \((n - 2, 2n - 5)\)。
- 第 \(n - 3\) 行涂色坐标为 \((n - 3, 1)\)。
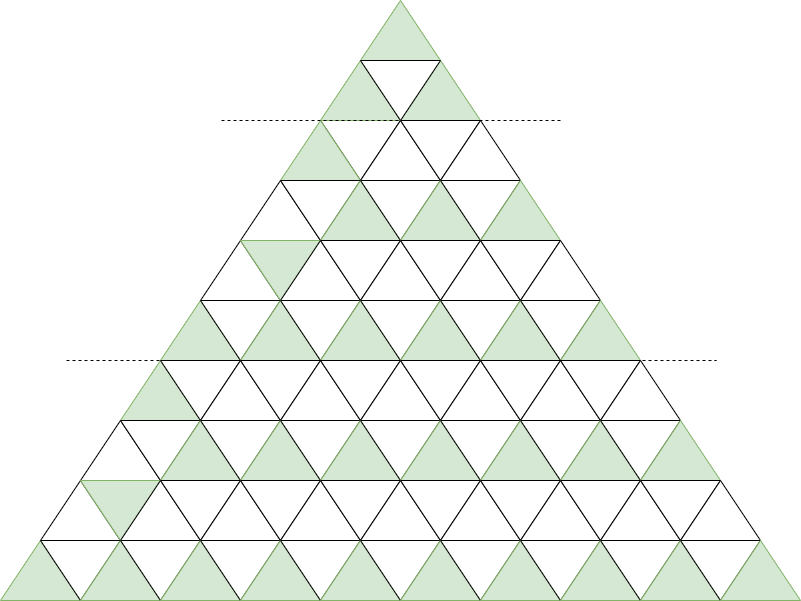
因此,我们可以按照上述规律,先给第一行涂色,然后从最后一行开始,每四行涂色一次,直到第二行结束。

时间复杂度 \((n^2)\),其中 \(n\) 为题目给定的参数。忽略答案数组的空间消耗,空间复杂度 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution:
def colorRed(self, n: int) -> List[List[int]]:
ans = [[1, 1]]
k = 0
for i in range(n, 1, -1):
if k == 0:
for j in range(1, i << 1, 2):
ans.append([i, j])
elif k == 1:
ans.append([i, 2])
elif k == 2:
for j in range(3, i << 1, 2):
ans.append([i, j])
else:
ans.append([i, 1])
k = (k + 1) % 4
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | class Solution {
public int[][] colorRed(int n) {
List<int[]> ans = new ArrayList<>();
ans.add(new int[] {1, 1});
for (int i = n, k = 0; i > 1; --i, k = (k + 1) % 4) {
if (k == 0) {
for (int j = 1; j < i << 1; j += 2) {
ans.add(new int[] {i, j});
}
} else if (k == 1) {
ans.add(new int[] {i, 2});
} else if (k == 2) {
for (int j = 3; j < i << 1; j += 2) {
ans.add(new int[] {i, j});
}
} else {
ans.add(new int[] {i, 1});
}
}
return ans.toArray(new int[0][]);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution {
public:
vector<vector<int>> colorRed(int n) {
vector<vector<int>> ans;
ans.push_back({1, 1});
for (int i = n, k = 0; i > 1; --i, k = (k + 1) % 4) {
if (k == 0) {
for (int j = 1; j < i << 1; j += 2) {
ans.push_back({i, j});
}
} else if (k == 1) {
ans.push_back({i, 2});
} else if (k == 2) {
for (int j = 3; j < i << 1; j += 2) {
ans.push_back({i, j});
}
} else {
ans.push_back({i, 1});
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | func colorRed(n int) (ans [][]int) {
ans = append(ans, []int{1, 1})
for i, k := n, 0; i > 1; i, k = i-1, (k+1)%4 {
if k == 0 {
for j := 1; j < i<<1; j += 2 {
ans = append(ans, []int{i, j})
}
} else if k == 1 {
ans = append(ans, []int{i, 2})
} else if k == 2 {
for j := 3; j < i<<1; j += 2 {
ans = append(ans, []int{i, j})
}
} else {
ans = append(ans, []int{i, 1})
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | function colorRed(n: number): number[][] {
const ans: number[][] = [[1, 1]];
for (let i = n, k = 0; i > 1; --i, k = (k + 1) % 4) {
if (k === 0) {
for (let j = 1; j < i << 1; j += 2) {
ans.push([i, j]);
}
} else if (k === 1) {
ans.push([i, 2]);
} else if (k === 2) {
for (let j = 3; j < i << 1; j += 2) {
ans.push([i, j]);
}
} else {
ans.push([i, 1]);
}
}
return ans;
}
|





