二叉树
哈希表
广度优先搜索
树
深度优先搜索
题目描述
给你一棵二叉树的根 root ,请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。
如果两个节点在树中有相同的深度且它们的父节点不同,那么它们互为 堂兄弟 。
请你返回修改值之后,树的根 root 。
注意 ,一个节点的深度指的是从树根节点到这个节点经过的边数。
示例 1:
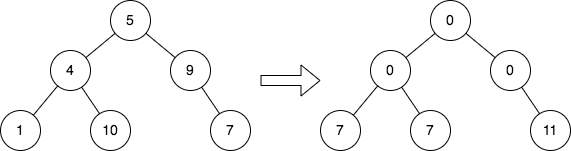
输入: root = [5,4,9,1,10,null,7]
输出: [0,0,0,7,7,null,11]
解释: 上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 5 的节点没有堂兄弟,所以值修改为 0 。
- 值为 4 的节点没有堂兄弟,所以值修改为 0 。
- 值为 9 的节点没有堂兄弟,所以值修改为 0 。
- 值为 1 的节点有一个堂兄弟,值为 7 ,所以值修改为 7 。
- 值为 10 的节点有一个堂兄弟,值为 7 ,所以值修改为 7 。
- 值为 7 的节点有两个堂兄弟,值分别为 1 和 10 ,所以值修改为 11 。
示例 2:
输入: root = [3,1,2]
输出: [0,0,0]
解释: 上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 3 的节点没有堂兄弟,所以值修改为 0 。
- 值为 1 的节点没有堂兄弟,所以值修改为 0 。
- 值为 2 的节点没有堂兄弟,所以值修改为 0 。
提示:
树中节点数目的范围是 [1, 105 ] 。
1 <= Node.val <= 104
解法
方法一:两次 DFS
我们创建一个列表 \(s\) 用于记录二叉树每一层的节点值之和,其中 \(s[depth]\) 表示第 \(depth\) 层的节点值之和(规定根节点所在的层为第 \(0\) 层)。
接下来,我们先跑一遍 DFS,计算出数组 \(s\) 的值。然后再跑一遍 DFS,更新每个节点的子节点的值,子节点的值等于子节点所在层的节点值之和减去子节点及其兄弟节点的值。
时间复杂度 \(O(n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 是二叉树的节点数。
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def replaceValueInTree ( self , root : Optional [ TreeNode ]) -> Optional [ TreeNode ]:
def dfs1 ( root : Optional [ TreeNode ], depth : int ):
if root is None :
return
if len ( s ) <= depth :
s . append ( 0 )
s [ depth ] += root . val
dfs1 ( root . left , depth + 1 )
dfs1 ( root . right , depth + 1 )
def dfs2 ( root : Optional [ TreeNode ], depth : int ):
sub = ( root . left . val if root . left else 0 ) + (
root . right . val if root . right else 0
)
depth += 1
if root . left :
root . left . val = s [ depth ] - sub
dfs2 ( root . left , depth )
if root . right :
root . right . val = s [ depth ] - sub
dfs2 ( root . right , depth )
s = []
dfs1 ( root , 0 )
root . val = 0
dfs2 ( root , 0 )
return root
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private List < Integer > s = new ArrayList <> ();
public TreeNode replaceValueInTree ( TreeNode root ) {
dfs1 ( root , 0 );
root . val = 0 ;
dfs2 ( root , 0 );
return root ;
}
private void dfs1 ( TreeNode root , int depth ) {
if ( root == null ) {
return ;
}
if ( s . size () <= depth ) {
s . add ( 0 );
}
s . set ( depth , s . get ( depth ) + root . val );
dfs1 ( root . left , depth + 1 );
dfs1 ( root . right , depth + 1 );
}
private void dfs2 ( TreeNode root , int depth ) {
int l = root . left == null ? 0 : root . left . val ;
int r = root . right == null ? 0 : root . right . val ;
int sub = l + r ;
++ depth ;
if ( root . left != null ) {
root . left . val = s . get ( depth ) - sub ;
dfs2 ( root . left , depth );
}
if ( root . right != null ) {
root . right . val = s . get ( depth ) - sub ;
dfs2 ( root . right , depth );
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
TreeNode * replaceValueInTree ( TreeNode * root ) {
memset ( s , 0 , sizeof ( s ));
dfs1 ( root , 0 );
root -> val = 0 ;
dfs2 ( root , 0 );
return root ;
}
private :
int s [ 100010 ];
void dfs1 ( TreeNode * root , int depth ) {
if ( ! root ) {
return ;
}
s [ depth ] += root -> val ;
dfs1 ( root -> left , depth + 1 );
dfs1 ( root -> right , depth + 1 );
};
void dfs2 ( TreeNode * root , int depth ) {
int l = root -> left ? root -> left -> val : 0 ;
int r = root -> right ? root -> right -> val : 0 ;
int sub = l + r ;
++ depth ;
if ( root -> left ) {
root -> left -> val = s [ depth ] - sub ;
dfs2 ( root -> left , depth );
}
if ( root -> right ) {
root -> right -> val = s [ depth ] - sub ;
dfs2 ( root -> right , depth );
}
};
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func replaceValueInTree ( root * TreeNode ) * TreeNode {
s := [] int {}
var dfs1 func ( * TreeNode , int )
dfs1 = func ( root * TreeNode , depth int ) {
if root == nil {
return
}
if len ( s ) <= depth {
s = append ( s , 0 )
}
s [ depth ] += root . Val
dfs1 ( root . Left , depth + 1 )
dfs1 ( root . Right , depth + 1 )
}
var dfs2 func ( * TreeNode , int )
dfs2 = func ( root * TreeNode , depth int ) {
l , r := 0 , 0
if root . Left != nil {
l = root . Left . Val
}
if root . Right != nil {
r = root . Right . Val
}
sub := l + r
depth ++
if root . Left != nil {
root . Left . Val = s [ depth ] - sub
dfs2 ( root . Left , depth )
}
if root . Right != nil {
root . Right . Val = s [ depth ] - sub
dfs2 ( root . Right , depth )
}
}
dfs1 ( root , 0 )
root . Val = 0
dfs2 ( root , 0 )
return root
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function replaceValueInTree ( root : TreeNode | null ) : TreeNode | null {
const s : number [] = [];
const dfs1 = ( root : TreeNode | null , depth : number ) => {
if ( ! root ) {
return ;
}
if ( s . length <= depth ) {
s . push ( 0 );
}
s [ depth ] += root . val ;
dfs1 ( root . left , depth + 1 );
dfs1 ( root . right , depth + 1 );
};
const dfs2 = ( root : TreeNode | null , depth : number ) => {
const sub = ( root . left ? . val || 0 ) + ( root . right ? . val || 0 );
++ depth ;
if ( root . left ) {
root . left . val = s [ depth ] - sub ;
dfs2 ( root . left , depth );
}
if ( root . right ) {
root . right . val = s [ depth ] - sub ;
dfs2 ( root . right , depth );
}
};
dfs1 ( root , 0 );
root . val = 0 ;
dfs2 ( root , 0 );
return root ;
}
方法二:BFS
我们先将根节点的值更新为 \(0\) ,用一个队列 \(q\) 来存储每一层的所有节点,初始时将根节点入队。
然后遍历队列,计算每一层的所有子节点的值之和 \(s\) ,然后计算每个子节点及其兄弟节点的值之和 \(sub\) ,然后更新每个子节点的值为 \(s - sub\) 。
遍历结束后,返回根节点即可。
时间复杂度 \(O(n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 是二叉树的节点数。
Python3 Java C++ Go TypeScript JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def replaceValueInTree ( self , root : Optional [ TreeNode ]) -> Optional [ TreeNode ]:
root . val = 0
q = [ root ]
while q :
t = []
s = 0
for node in q :
if node . left :
t . append ( node . left )
s += node . left . val
if node . right :
t . append ( node . right )
s += node . right . val
for node in q :
sub = ( node . left . val if node . left else 0 ) + (
node . right . val if node . right else 0
)
if node . left :
node . left . val = s - sub
if node . right :
node . right . val = s - sub
q = t
return root
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode replaceValueInTree ( TreeNode root ) {
root . val = 0 ;
List < TreeNode > q = List . of ( root );
while ( ! q . isEmpty ()) {
List < TreeNode > t = new ArrayList <> ();
int s = 0 ;
for ( TreeNode node : q ) {
if ( node . left != null ) {
t . add ( node . left );
s += node . left . val ;
}
if ( node . right != null ) {
t . add ( node . right );
s += node . right . val ;
}
}
for ( TreeNode node : q ) {
int sub = ( node . left == null ? 0 : node . left . val )
+ ( node . right == null ? 0 : node . right . val );
if ( node . left != null ) {
node . left . val = s - sub ;
}
if ( node . right != null ) {
node . right . val = s - sub ;
}
}
q = t ;
}
return root ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
TreeNode * replaceValueInTree ( TreeNode * root ) {
root -> val = 0 ;
vector < TreeNode *> q = { root };
while ( ! q . empty ()) {
vector < TreeNode *> t ;
int s = 0 ;
for ( TreeNode * node : q ) {
if ( node -> left ) {
t . emplace_back ( node -> left );
s += node -> left -> val ;
}
if ( node -> right ) {
t . emplace_back ( node -> right );
s += node -> right -> val ;
}
}
for ( TreeNode * node : q ) {
int sub = ( node -> left ? node -> left -> val : 0 ) + ( node -> right ? node -> right -> val : 0 );
if ( node -> left ) {
node -> left -> val = s - sub ;
}
if ( node -> right ) {
node -> right -> val = s - sub ;
}
}
q = move ( t );
}
return root ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func replaceValueInTree ( root * TreeNode ) * TreeNode {
root . Val = 0
q := [] * TreeNode { root }
for len ( q ) > 0 {
t := [] * TreeNode {}
s := 0
for _ , node := range q {
if node . Left != nil {
t = append ( t , node . Left )
s += node . Left . Val
}
if node . Right != nil {
t = append ( t , node . Right )
s += node . Right . Val
}
}
for _ , node := range q {
sub := 0
if node . Left != nil {
sub += node . Left . Val
}
if node . Right != nil {
sub += node . Right . Val
}
if node . Left != nil {
node . Left . Val = s - sub
}
if node . Right != nil {
node . Right . Val = s - sub
}
}
q = t
}
return root
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function replaceValueInTree ( root : TreeNode | null ) : TreeNode | null {
let q = [ root ];
let [ sum , nextSum ] = [ 0 , root . val ];
while ( q . length ) {
const qNext : TreeNode [] = [];
[ sum , nextSum ] = [ nextSum , 0 ];
for ( const node of q ) {
const x = ( node . left ? . val ?? 0 ) + ( node . right ? . val ?? 0 );
node . val = sum - node . val ;
nextSum += x ;
if ( node . left ) {
node . left . val = x ;
qNext . push ( node . left );
}
if ( node . right ) {
node . right . val = x ;
qNext . push ( node . right );
}
}
q = qNext ;
}
return root ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 function replaceValueInTree ( root ) {
let q = [ root ];
let [ sum , nextSum ] = [ 0 , root . val ];
while ( q . length ) {
const qNext = [];
[ sum , nextSum ] = [ nextSum , 0 ];
for ( const node of q ) {
const x = ( node . left ? . val ?? 0 ) + ( node . right ? . val ?? 0 );
node . val = sum - node . val ;
nextSum += x ;
if ( node . left ) {
node . left . val = x ;
qNext . push ( node . left );
}
if ( node . right ) {
node . right . val = x ;
qNext . push ( node . right );
}
}
q = qNext ;
}
return root ;
}
GitHub