


题目描述
给你一个下标从 0 开始的二维整数数组 nums 。
返回位于 nums 至少一条 对角线 上的最大 质数 。如果任一对角线上均不存在质数,返回 0 。
注意:
- 如果某个整数大于
1 ,且不存在除 1 和自身之外的正整数因子,则认为该整数是一个质数。
- 如果存在整数
i ,使得 nums[i][i] = val 或者 nums[i][nums.length - i - 1]= val ,则认为整数 val 位于 nums 的一条对角线上。
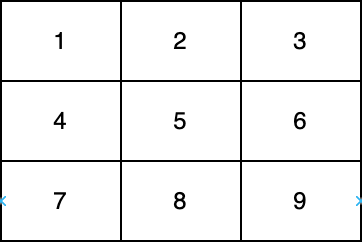
在上图中,一条对角线是 [1,5,9] ,而另一条对角线是 [3,5,7] 。
示例 1:
输入:nums = [[1,2,3],[5,6,7],[9,10,11]]
输出:11
解释:数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数,故返回 11 。
示例 2:
输入:nums = [[1,2,3],[5,17,7],[9,11,10]]
输出:17
解释:数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数,故返回 17 。
提示:
1 <= nums.length <= 300nums.length == numsi.length1 <= nums[i][j] <= 4*106
解法
方法一:数学 + 模拟
我们实现一个函数 is_prime,判断一个数是否为质数。
然后遍历数组,判断对角线上的数是否为质数,如果是,更新答案。
时间复杂度 \(O(n \times \sqrt{M})\),其中 \(n\) 和 \(M\) 分别为数组的行数和数组中的最大值。空间复杂度 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | class Solution:
def diagonalPrime(self, nums: List[List[int]]) -> int:
def is_prime(x: int) -> bool:
if x < 2:
return False
return all(x % i for i in range(2, int(sqrt(x)) + 1))
n = len(nums)
ans = 0
for i, row in enumerate(nums):
if is_prime(row[i]):
ans = max(ans, row[i])
if is_prime(row[n - i - 1]):
ans = max(ans, row[n - i - 1])
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
public int diagonalPrime(int[][] nums) {
int n = nums.length;
int ans = 0;
for (int i = 0; i < n; ++i) {
if (isPrime(nums[i][i])) {
ans = Math.max(ans, nums[i][i]);
}
if (isPrime(nums[i][n - i - 1])) {
ans = Math.max(ans, nums[i][n - i - 1]);
}
}
return ans;
}
private boolean isPrime(int x) {
if (x < 2) {
return false;
}
for (int i = 2; i <= x / i; ++i) {
if (x % i == 0) {
return false;
}
}
return true;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | class Solution {
public:
int diagonalPrime(vector<vector<int>>& nums) {
int n = nums.size();
int ans = 0;
for (int i = 0; i < n; ++i) {
if (isPrime(nums[i][i])) {
ans = max(ans, nums[i][i]);
}
if (isPrime(nums[i][n - i - 1])) {
ans = max(ans, nums[i][n - i - 1]);
}
}
return ans;
}
bool isPrime(int x) {
if (x < 2) {
return false;
}
for (int i = 2; i <= x / i; ++i) {
if (x % i == 0) {
return false;
}
}
return true;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | func diagonalPrime(nums [][]int) (ans int) {
n := len(nums)
for i, row := range nums {
if isPrime(row[i]) {
ans = max(ans, row[i])
}
if isPrime(row[n-i-1]) {
ans = max(ans, row[n-i-1])
}
}
return
}
func isPrime(x int) bool {
if x < 2 {
return false
}
for i := 2; i <= x/i; i++ {
if x%i == 0 {
return false
}
}
return true
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 | impl Solution {
pub fn diagonal_prime(nums: Vec<Vec<i32>>) -> i32 {
let mut ans = 0;
let n = nums.len();
for (i, row) in nums.iter().enumerate() {
if Self::is_prime(row[i]) && row[i] > ans {
ans = row[i];
}
if Self::is_prime(row[n - i - 1]) && row[n - i - 1] > ans {
ans = row[n - i - 1];
}
}
ans
}
fn is_prime(n: i32) -> bool {
if n < 2 {
return false;
}
let upper = (n as f64).sqrt() as i32;
for i in 2..=upper {
if n % i == 0 {
return false;
}
}
true
}
}
|



