图
拓扑排序
数组
树
题目描述
给你一个 n 个节点的无向无根树,节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai , bi ] 表示树中节点 ai 和 bi 之间有一条边。再给你一个长度为 n 的数组 coins ,其中 coins[i] 可能为 0 也可能为 1 ,1 表示节点 i 处有一个金币。
一开始,你需要选择树中任意一个节点出发。你可以执行下述操作任意次:
收集距离当前节点距离为 2 以内的所有金币,或者
移动到树中一个相邻节点。
你需要收集树中所有的金币,并且回到出发节点,请你返回最少经过的边数。
如果你多次经过一条边,每一次经过都会给答案加一。
示例 1:
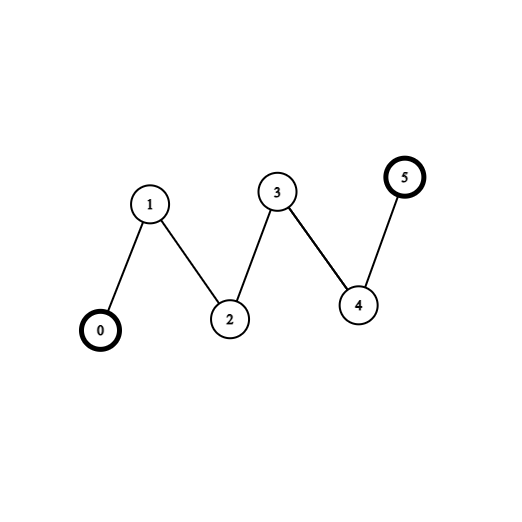
输入: coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
输出: 2
解释: 从节点 2 出发,收集节点 0 处的金币,移动到节点 3 ,收集节点 5 处的金币,然后移动回节点 2 。
示例 2:
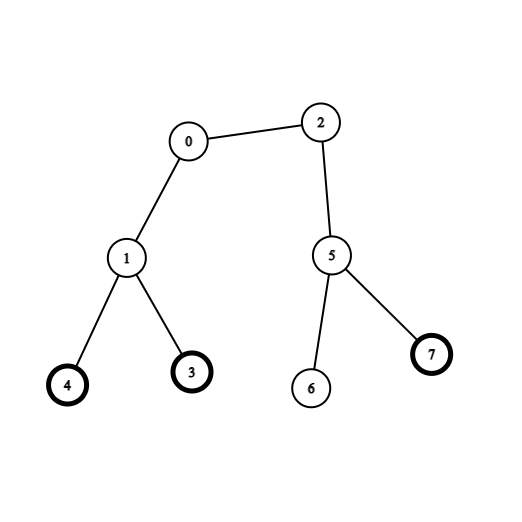
输入: coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
输出: 2
解释: 从节点 0 出发,收集节点 4 和 3 处的金币,移动到节点 2 处,收集节点 7 处的金币,移动回节点 0 。
提示:
n == coins.length1 <= n <= 3 * 104 0 <= coins[i] <= 1edges.length == n - 1edges[i].length == 20 <= ai , bi < nai != bi edges 表示一棵合法的树。
解法
方法一:拓扑排序
我们先将 \(edges\) 中的边转换成邻接表 \(g\) ,其中 \(g[i]\) 表示节点 \(i\) 的所有邻接节点,用集合表示。
接下来我们遍历所有节点,找到 \(coins[i]=0\) 且 \(g[i]\) 中只有一个节点的节点(也即是金币为 \(0\) 的叶子节点),将其加入队列 \(q\) 中。
然后我们不断地从队列中取出节点,将其从邻接表中删除,然后判断其邻接节点是否满足 \(coins[j]=0\) 且 \(g[j]\) 中只有一个节点的条件,如果满足则将其加入队列 \(q\) 中。循环,直至队列为空。
经过上述操作后,我们得到了一棵新的树,且树的叶子节点都是金币为 \(1\) 的节点。
然后,我们再删除剩下的两层叶子节点,最终得到的是一棵所有节点都需要被访问的节点,我们只需要统计其边数,乘上 \(2\) ,即为答案。
时间复杂度 \(O(n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 为节点数。
相似题目:
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 class Solution :
def collectTheCoins ( self , coins : List [ int ], edges : List [ List [ int ]]) -> int :
g = defaultdict ( set )
for a , b in edges :
g [ a ] . add ( b )
g [ b ] . add ( a )
n = len ( coins )
q = deque ( i for i in range ( n ) if len ( g [ i ]) == 1 and coins [ i ] == 0 )
while q :
i = q . popleft ()
for j in g [ i ]:
g [ j ] . remove ( i )
if coins [ j ] == 0 and len ( g [ j ]) == 1 :
q . append ( j )
g [ i ] . clear ()
for k in range ( 2 ):
q = [ i for i in range ( n ) if len ( g [ i ]) == 1 ]
for i in q :
for j in g [ i ]:
g [ j ] . remove ( i )
g [ i ] . clear ()
return sum ( len ( g [ a ]) > 0 and len ( g [ b ]) > 0 for a , b in edges ) * 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50 class Solution {
public int collectTheCoins ( int [] coins , int [][] edges ) {
int n = coins . length ;
Set < Integer >[] g = new Set [ n ] ;
Arrays . setAll ( g , k -> new HashSet <> ());
for ( var e : edges ) {
int a = e [ 0 ] , b = e [ 1 ] ;
g [ a ] . add ( b );
g [ b ] . add ( a );
}
Deque < Integer > q = new ArrayDeque <> ();
for ( int i = 0 ; i < n ; ++ i ) {
if ( coins [ i ] == 0 && g [ i ] . size () == 1 ) {
q . offer ( i );
}
}
while ( ! q . isEmpty ()) {
int i = q . poll ();
for ( int j : g [ i ] ) {
g [ j ] . remove ( i );
if ( coins [ j ] == 0 && g [ j ] . size () == 1 ) {
q . offer ( j );
}
}
g [ i ] . clear ();
}
q . clear ();
for ( int k = 0 ; k < 2 ; ++ k ) {
for ( int i = 0 ; i < n ; ++ i ) {
if ( g [ i ] . size () == 1 ) {
q . offer ( i );
}
}
for ( int i : q ) {
for ( int j : g [ i ] ) {
g [ j ] . remove ( i );
}
g [ i ] . clear ();
}
}
int ans = 0 ;
for ( var e : edges ) {
int a = e [ 0 ] , b = e [ 1 ] ;
if ( g [ a ] . size () > 0 && g [ b ] . size () > 0 ) {
ans += 2 ;
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 class Solution {
public :
int collectTheCoins ( vector < int >& coins , vector < vector < int >>& edges ) {
int n = coins . size ();
unordered_set < int > g [ n ];
for ( auto & e : edges ) {
int a = e [ 0 ], b = e [ 1 ];
g [ a ]. insert ( b );
g [ b ]. insert ( a );
}
queue < int > q ;
for ( int i = 0 ; i < n ; ++ i ) {
if ( coins [ i ] == 0 && g [ i ]. size () == 1 ) {
q . push ( i );
}
}
while ( ! q . empty ()) {
int i = q . front ();
q . pop ();
for ( int j : g [ i ]) {
g [ j ]. erase ( i );
if ( coins [ j ] == 0 && g [ j ]. size () == 1 ) {
q . push ( j );
}
}
g [ i ]. clear ();
}
for ( int k = 0 ; k < 2 ; ++ k ) {
vector < int > q ;
for ( int i = 0 ; i < n ; ++ i ) {
if ( g [ i ]. size () == 1 ) {
q . push_back ( i );
}
}
for ( int i : q ) {
for ( int j : g [ i ]) {
g [ j ]. erase ( i );
}
g [ i ]. clear ();
}
}
int ans = 0 ;
for ( auto & e : edges ) {
int a = e [ 0 ], b = e [ 1 ];
if ( g [ a ]. size () && g [ b ]. size ()) {
ans += 2 ;
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 func collectTheCoins ( coins [] int , edges [][] int ) int {
n := len ( coins )
g := make ([] map [ int ] bool , n )
for i := range g {
g [ i ] = map [ int ] bool {}
}
for _ , e := range edges {
a , b := e [ 0 ], e [ 1 ]
g [ a ][ b ] = true
g [ b ][ a ] = true
}
q := [] int {}
for i , c := range coins {
if c == 0 && len ( g [ i ]) == 1 {
q = append ( q , i )
}
}
for len ( q ) > 0 {
i := q [ 0 ]
q = q [ 1 :]
for j := range g [ i ] {
delete ( g [ j ], i )
if coins [ j ] == 0 && len ( g [ j ]) == 1 {
q = append ( q , j )
}
}
g [ i ] = map [ int ] bool {}
}
for k := 0 ; k < 2 ; k ++ {
q := [] int {}
for i := range coins {
if len ( g [ i ]) == 1 {
q = append ( q , i )
}
}
for _ , i := range q {
for j := range g [ i ] {
delete ( g [ j ], i )
}
g [ i ] = map [ int ] bool {}
}
}
ans := 0
for _ , e := range edges {
a , b := e [ 0 ], e [ 1 ]
if len ( g [ a ]) > 0 && len ( g [ b ]) > 0 {
ans += 2
}
}
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 function collectTheCoins ( coins : number [], edges : number [][]) : number {
const n = coins . length ;
const g : Set < number > [] = new Array ( n ). fill ( 0 ). map (() => new Set < number > ());
for ( const [ a , b ] of edges ) {
g [ a ]. add ( b );
g [ b ]. add ( a );
}
let q : number [] = [];
for ( let i = 0 ; i < n ; ++ i ) {
if ( coins [ i ] === 0 && g [ i ]. size === 1 ) {
q . push ( i );
}
}
while ( q . length ) {
const i = q . pop () ! ;
for ( const j of g [ i ]) {
g [ j ]. delete ( i );
if ( coins [ j ] === 0 && g [ j ]. size === 1 ) {
q . push ( j );
}
}
g [ i ]. clear ();
}
q = [];
for ( let k = 0 ; k < 2 ; ++ k ) {
for ( let i = 0 ; i < n ; ++ i ) {
if ( g [ i ]. size === 1 ) {
q . push ( i );
}
}
for ( const i of q ) {
for ( const j of g [ i ]) {
g [ j ]. delete ( i );
}
g [ i ]. clear ();
}
}
let ans = 0 ;
for ( const [ a , b ] of edges ) {
if ( g [ a ]. size > 0 && g [ b ]. size > 0 ) {
ans += 2 ;
}
}
return ans ;
}
GitHub