


题目描述
Alice 有一棵 n 个节点的树,节点编号为 0 到 n - 1 。树用一个长度为 n - 1 的二维整数数组 edges 表示,其中 edges[i] = [ai, bi] ,表示树中节点 ai 和 bi 之间有一条边。
Alice 想要 Bob 找到这棵树的根。她允许 Bob 对这棵树进行若干次 猜测 。每一次猜测,Bob 做如下事情:
- 选择两个 不相等 的整数
u 和 v ,且树中必须存在边 [u, v] 。
- Bob 猜测树中
u 是 v 的 父节点 。
Bob 的猜测用二维整数数组 guesses 表示,其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父节点。
Alice 非常懒,她不想逐个回答 Bob 的猜测,只告诉 Bob 这些猜测里面 至少 有 k 个猜测的结果为 true 。
给你二维整数数组 edges ,Bob 的所有猜测和整数 k ,请你返回可能成为树根的 节点数目 。如果没有这样的树,则返回 0。
示例 1:
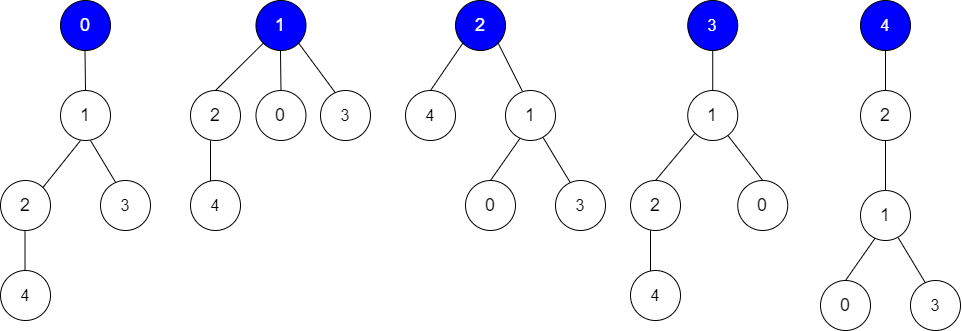
输入:edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
输出:3
解释:
根为节点 0 ,正确的猜测为 [1,3], [0,1], [2,4]
根为节点 1 ,正确的猜测为 [1,3], [1,0], [2,4]
根为节点 2 ,正确的猜测为 [1,3], [1,0], [2,4]
根为节点 3 ,正确的猜测为 [1,0], [2,4]
根为节点 4 ,正确的猜测为 [1,3], [1,0]
节点 0 ,1 或 2 为根时,可以得到 3 个正确的猜测。
示例 2:
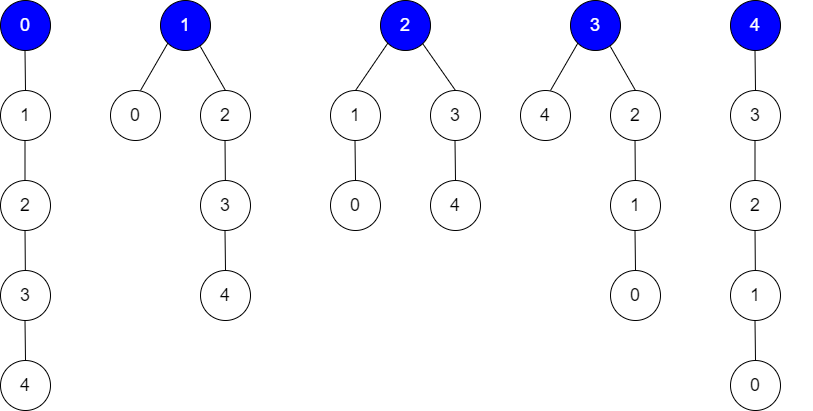
输入:edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1
输出:5
解释:
根为节点 0 ,正确的猜测为 [3,4]
根为节点 1 ,正确的猜测为 [1,0], [3,4]
根为节点 2 ,正确的猜测为 [1,0], [2,1], [3,4]
根为节点 3 ,正确的猜测为 [1,0], [2,1], [3,2], [3,4]
根为节点 4 ,正确的猜测为 [1,0], [2,1], [3,2]
任何节点为根,都至少有 1 个正确的猜测。
提示:
edges.length == n - 12 <= n <= 1051 <= guesses.length <= 1050 <= ai, bi, uj, vj <= n - 1ai != biuj != vjedges 表示一棵有效的树。guesses[j] 是树中的一条边。guesses 是唯一的。0 <= k <= guesses.length
解法
方法一:树形 DP(换根)
我们先遍历题目给定的边集合 \(edges\),将其转换为邻接表 \(g\),其中 \(g[i]\) 表示节点 \(i\) 的所有邻接节点。用哈希表 \(gs\) 记录题目给定的猜测集合 \(guesses\)。
接下来,我们先从节点 \(0\) 开始,进行一次 DFS,统计从节点 \(0\) 出发,能够到达的所有节点中,有多少条边在 \(guesses\) 中。我们用变量 \(cnt\) 记录这个数量。
然后,我们再从节点 \(0\) 开始,进行一次 DFS,统计以每个点为根的树中,有多少条边在 \(guesses\) 中。如果这个数量大于等于 \(k\),则说明该节点是一个可能的根节点,我们将答案加 \(1\)。
因此,问题就转化为了求以每个点为根的树中,有多少条边在 \(guesses\) 中。我们已经知道了从节点 \(0\) 出发,能够到达的所有节点中,有多少条边在 \(guesses\) 中,即 \(cnt\)。我们可以通过在 DFS 中,将 \(cnt\) 的值加上或减去当前边是否在 \(guesses\) 中,来维护这个值。
假设我们当前遍历到节点 \(i\),此时 \(cnt\) 表示以 \(i\) 为根节点,有多少条边在 \(guesses\) 中。那么对于 \(i\) 的每个邻接节点 \(j\),我们要计算以 \(j\) 为根节点,有多少条边在 \(guesses\) 中。如果 \((i, j)\) 在 \(guesses\) 中,那么以 \(j\) 为根节点的,就不存在 \((i, j)\) 这条边,因此 \(cnt\) 的值要减去 \(1\)。如果 \((j, i)\) 在 \(guesses\) 中,那么以 \(j\) 为根节点的,要多出一条 \((i, j)\) 这条边,因此 \(cnt\) 的值要加上 \(1\)。即 \(f[j] = f[i] + (j, i) \in guesses - (i, j) \in guesses\)。其中 \(f[i]\) 表示以 \(i\) 为根节点,有多少条边在 \(guesses\) 中。
时间复杂度 \(O(n + m)\),空间复杂度 \(O(n + m)\)。其中 \(n\) 和 \(m\) 分别为 \(edges\) 和 \(guesses\) 的长度。
相似题目:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 | class Solution:
def rootCount(
self, edges: List[List[int]], guesses: List[List[int]], k: int
) -> int:
def dfs1(i, fa):
nonlocal cnt
for j in g[i]:
if j != fa:
cnt += gs[(i, j)]
dfs1(j, i)
def dfs2(i, fa):
nonlocal ans, cnt
ans += cnt >= k
for j in g[i]:
if j != fa:
cnt -= gs[(i, j)]
cnt += gs[(j, i)]
dfs2(j, i)
cnt -= gs[(j, i)]
cnt += gs[(i, j)]
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
gs = Counter((u, v) for u, v in guesses)
cnt = 0
dfs1(0, -1)
ans = 0
dfs2(0, -1)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 | class Solution {
private List<Integer>[] g;
private Map<Long, Integer> gs = new HashMap<>();
private int ans;
private int k;
private int cnt;
private int n;
public int rootCount(int[][] edges, int[][] guesses, int k) {
this.k = k;
n = edges.length + 1;
g = new List[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
for (var e : guesses) {
int a = e[0], b = e[1];
gs.merge(f(a, b), 1, Integer::sum);
}
dfs1(0, -1);
dfs2(0, -1);
return ans;
}
private void dfs1(int i, int fa) {
for (int j : g[i]) {
if (j != fa) {
cnt += gs.getOrDefault(f(i, j), 0);
dfs1(j, i);
}
}
}
private void dfs2(int i, int fa) {
ans += cnt >= k ? 1 : 0;
for (int j : g[i]) {
if (j != fa) {
int a = gs.getOrDefault(f(i, j), 0);
int b = gs.getOrDefault(f(j, i), 0);
cnt -= a;
cnt += b;
dfs2(j, i);
cnt -= b;
cnt += a;
}
}
}
private long f(int i, int j) {
return 1L * i * n + j;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 | class Solution {
public:
int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int k) {
int n = edges.size() + 1;
vector<int> g[n];
unordered_map<long long, int> gs;
auto f = [&](int i, int j) {
return 1LL * i * n + j;
};
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
for (auto& e : guesses) {
int a = e[0], b = e[1];
gs[f(a, b)]++;
}
int ans = 0;
int cnt = 0;
function<void(int, int)> dfs1 = [&](int i, int fa) {
for (int& j : g[i]) {
if (j != fa) {
cnt += gs[f(i, j)];
dfs1(j, i);
}
}
};
function<void(int, int)> dfs2 = [&](int i, int fa) {
ans += cnt >= k;
for (int& j : g[i]) {
if (j != fa) {
int a = gs[f(i, j)];
int b = gs[f(j, i)];
cnt -= a;
cnt += b;
dfs2(j, i);
cnt -= b;
cnt += a;
}
}
};
dfs1(0, -1);
dfs2(0, -1);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 | func rootCount(edges [][]int, guesses [][]int, k int) (ans int) {
n := len(edges) + 1
g := make([][]int, n)
gs := map[int]int{}
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
f := func(i, j int) int {
return i*n + j
}
for _, e := range guesses {
a, b := e[0], e[1]
gs[f(a, b)]++
}
cnt := 0
var dfs1 func(i, fa int)
var dfs2 func(i, fa int)
dfs1 = func(i, fa int) {
for _, j := range g[i] {
if j != fa {
cnt += gs[f(i, j)]
dfs1(j, i)
}
}
}
dfs2 = func(i, fa int) {
if cnt >= k {
ans++
}
for _, j := range g[i] {
if j != fa {
a, b := gs[f(i, j)], gs[f(j, i)]
cnt -= a
cnt += b
dfs2(j, i)
cnt -= b
cnt += a
}
}
}
dfs1(0, -1)
dfs2(0, -1)
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | function rootCount(edges: number[][], guesses: number[][], k: number): number {
const n = edges.length + 1;
const g: number[][] = Array.from({ length: n }, () => []);
const gs: Map<number, number> = new Map();
const f = (i: number, j: number) => i * n + j;
for (const [a, b] of edges) {
g[a].push(b);
g[b].push(a);
}
for (const [a, b] of guesses) {
const x = f(a, b);
gs.set(x, gs.has(x) ? gs.get(x)! + 1 : 1);
}
let ans = 0;
let cnt = 0;
const dfs1 = (i: number, fa: number): void => {
for (const j of g[i]) {
if (j !== fa) {
cnt += gs.get(f(i, j)) || 0;
dfs1(j, i);
}
}
};
const dfs2 = (i: number, fa: number): void => {
ans += cnt >= k ? 1 : 0;
for (const j of g[i]) {
if (j !== fa) {
const a = gs.get(f(i, j)) || 0;
const b = gs.get(f(j, i)) || 0;
cnt -= a;
cnt += b;
dfs2(j, i);
cnt -= b;
cnt += a;
}
}
};
dfs1(0, -1);
dfs2(0, -1);
return ans;
}
|




