跳转至

2579. 统计染色格子数

题目描述

有一个无穷大的二维网格图，一开始所有格子都未染色。给你一个正整数 n ，表示你需要执行以下步骤 n 分钟：

  • 第一分钟，将 任一 格子染成蓝色。
  • 之后的每一分钟，将与蓝色格子相邻的 所有 未染色格子染成蓝色。

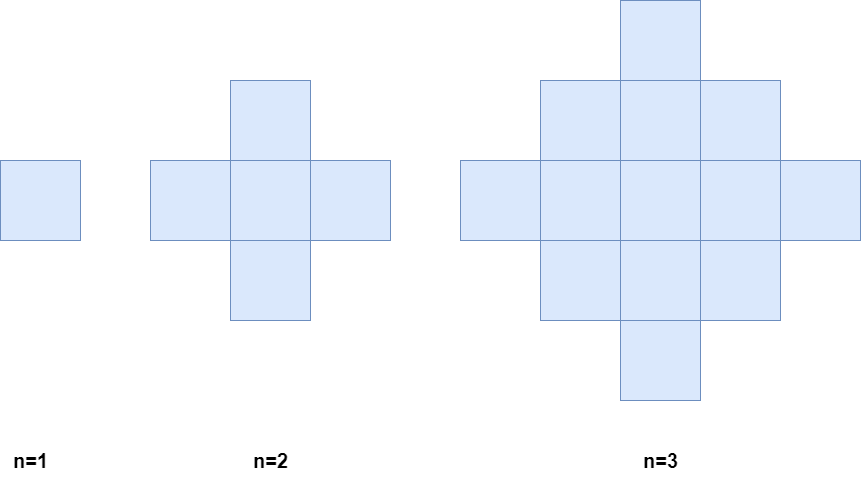
下图分别是 1、2、3 分钟后的网格图。

请你返回 n 分钟之后 被染色的格子 数目。

 

示例 1：

输入：n = 1
输出：1
解释：1 分钟后，只有 1 个蓝色的格子，所以返回 1 。

示例 2：

输入：n = 2
输出：5
解释：2 分钟后，有 4 个在边缘的蓝色格子和 1 个在中间的蓝色格子，所以返回 5 。

 

提示：

  • 1 <= n <= 105

解法

方法一：数学

我们观察发现，第 $n$ 分钟后，网格中共有 $2 \times n - 1$ 列，每一列上的数字分别为 $1, 3, 5, \cdots, 2 \times n - 1, 2 \times n - 3, \cdots, 3, 1$。左右两部分均为等差数列，求和可以得到答案 $2 \times n \times (n - 1) + 1$。

时间复杂度 $O(1)$，空间复杂度 $O(1)$。

1
2
3
class Solution:
    def coloredCells(self, n: int) -> int:
        return 2 * n * (n - 1) + 1

1
2
3
4
5
class Solution {
    public long coloredCells(int n) {
        return 2L * n * (n - 1) + 1;
    }
}

1
2
3
4
5
6
class Solution {
public:
    long long coloredCells(int n) {
        return 2LL * n * (n - 1) + 1;
    }
};

1
2
3
func coloredCells(n int) int64 {
    return int64(2*n*(n-1) + 1)
}

1
2
3
function coloredCells(n: number): number {
    return 2 * n * (n - 1) + 1;
}

1
2
3
4
5
impl Solution {
    pub fn colored_cells(n: i32) -> i64 {
        2 * (n as i64) * ((n as i64) - 1) + 1
    }
}

评论