


题目描述
给你一个下标从 0 开始的 m x n 二进制 矩阵 grid 。你可以从一个格子 (row, col) 移动到格子 (row + 1, col) 或者 (row, col + 1) ,前提是前往的格子值为 1 。如果从 (0, 0) 到 (m - 1, n - 1) 没有任何路径,我们称该矩阵是 不连通 的。
你可以翻转 最多一个 格子的值(也可以不翻转)。你 不能翻转 格子 (0, 0) 和 (m - 1, n - 1) 。
如果可以使矩阵不连通,请你返回 true ,否则返回 false 。
注意 ,翻转一个格子的值,可以使它的值从 0 变 1 ,或从 1 变 0 。
示例 1:
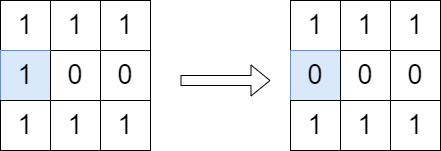
输入:grid = [[1,1,1],[1,0,0],[1,1,1]]
输出:true
解释:按照上图所示我们翻转蓝色格子里的值,翻转后从 (0, 0) 到 (2, 2) 没有路径。
示例 2:
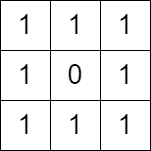
输入:grid = [[1,1,1],[1,0,1],[1,1,1]]
输出:false
解释:无法翻转至多一个格子,使 (0, 0) 到 (2, 2) 没有路径。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 105grid[0][0] == grid[m - 1][n - 1] == 1
解法
方法一:两次 DFS
我们先进行一次 DFS,判断从 \((0, 0)\) 到 \((m - 1, n - 1)\) 是否存在路径,记结果为 \(a\)。在 DFS 的过程中,我们将访问过的格子的值置为 \(0\),以防止重复访问。
接下来,我们将 \((0, 0)\) 和 \((m - 1, n - 1)\) 的值置为 \(1\),再进行一次 DFS,判断从 \((0, 0)\) 到 \((m - 1, n - 1)\) 是否存在路径,记结果为 \(b\)。在 DFS 的过程中,我们将访问过的格子的值置为 \(0\),避免重复访问。
最后,如果 \(a\) 和 \(b\) 都为 true,则返回 false,否则返回 true。
时间复杂度 \(O(m \times n)\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | class Solution:
def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:
def dfs(i, j):
if i >= m or j >= n or grid[i][j] == 0:
return False
grid[i][j] = 0
if i == m - 1 and j == n - 1:
return True
return dfs(i + 1, j) or dfs(i, j + 1)
m, n = len(grid), len(grid[0])
a = dfs(0, 0)
grid[0][0] = grid[-1][-1] = 1
b = dfs(0, 0)
return not (a and b)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
private int[][] grid;
private int m;
private int n;
public boolean isPossibleToCutPath(int[][] grid) {
this.grid = grid;
m = grid.length;
n = grid[0].length;
boolean a = dfs(0, 0);
grid[0][0] = 1;
grid[m - 1][n - 1] = 1;
boolean b = dfs(0, 0);
return !(a && b);
}
private boolean dfs(int i, int j) {
if (i >= m || j >= n || grid[i][j] == 0) {
return false;
}
if (i == m - 1 && j == n - 1) {
return true;
}
grid[i][j] = 0;
return dfs(i + 1, j) || dfs(i, j + 1);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution {
public:
bool isPossibleToCutPath(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
function<bool(int, int)> dfs = [&](int i, int j) -> bool {
if (i >= m || j >= n || grid[i][j] == 0) {
return false;
}
if (i == m - 1 && j == n - 1) {
return true;
}
grid[i][j] = 0;
return dfs(i + 1, j) || dfs(i, j + 1);
};
bool a = dfs(0, 0);
grid[0][0] = grid[m - 1][n - 1] = 1;
bool b = dfs(0, 0);
return !(a && b);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | func isPossibleToCutPath(grid [][]int) bool {
m, n := len(grid), len(grid[0])
var dfs func(i, j int) bool
dfs = func(i, j int) bool {
if i >= m || j >= n || grid[i][j] == 0 {
return false
}
if i == m-1 && j == n-1 {
return true
}
grid[i][j] = 0
return dfs(i+1, j) || dfs(i, j+1)
}
a := dfs(0, 0)
grid[0][0], grid[m-1][n-1] = 1, 1
b := dfs(0, 0)
return !(a && b)
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | function isPossibleToCutPath(grid: number[][]): boolean {
const m = grid.length;
const n = grid[0].length;
const dfs = (i: number, j: number): boolean => {
if (i >= m || j >= n || grid[i][j] !== 1) {
return false;
}
grid[i][j] = 0;
if (i === m - 1 && j === n - 1) {
return true;
}
return dfs(i + 1, j) || dfs(i, j + 1);
};
const a = dfs(0, 0);
grid[0][0] = 1;
grid[m - 1][n - 1] = 1;
const b = dfs(0, 0);
return !(a && b);
}
|




