跳转至

2550. 猴子碰撞的方法数

题目描述

现在有一个正凸多边形，其上共有 n 个顶点。顶点按顺时针方向从 0 到 n - 1 依次编号。每个顶点上 正好有一只猴子 。下图中是一个 6 个顶点的凸多边形。

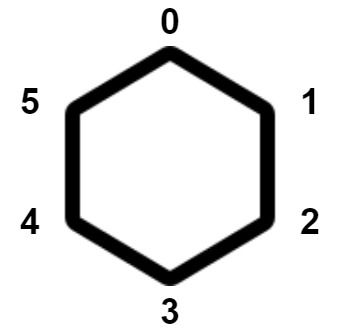
每个猴子同时移动到相邻的顶点。顶点 i 的相邻顶点可以是：

  • 顺时针方向的顶点 (i + 1) % n ，或
  • 逆时针方向的顶点 (i - 1 + n) % n 。

如果移动后至少有两只猴子停留在同一个顶点上或者相交在一条边上，则会发生 碰撞 。

返回猴子至少发生 一次碰撞 的移动方法数。由于答案可能非常大，请返回对 109+7 取余后的结果。

注意，每只猴子只能移动一次。

 

示例 1：

输入：n = 3
输出：6
解释：共计 8 种移动方式。
下面列出两种会发生碰撞的方式：
- 猴子 1 顺时针移动；猴子 2 逆时针移动；猴子 3 顺时针移动。猴子 1 和猴子 2 碰撞。
- 猴子 1 逆时针移动；猴子 2 逆时针移动；猴子 3 顺时针移动。猴子 1 和猴子 3 碰撞。
可以证明，有 6 种让猴子碰撞的方法。

示例 2：

输入：n = 4
输出：14
解释：可以证明，有 14 种让猴子碰撞的方法。

 

提示：

  • 3 <= n <= 109

解法

方法一：数学（快速幂）

根据题目描述，每一只猴子都有两种移动方式，即顺时针或逆时针。因此，一共有 $2^n$ 种移动方式。不碰撞的移动方式只有两种，即所有猴子都顺时针移动或所有猴子都逆时针移动。因此，碰撞的移动方式有 $2^n - 2$ 种。

我们可以用快速幂求出 $2^n$ 的值，然后用 $2^n - 2$ 求出碰撞的移动方式数，最后对 $10^9 + 7$ 取余即可。

时间复杂度 $O(\log n)$，其中 $n$ 为猴子的数量。空间复杂度 $O(1)$。

1
2
3
4
class Solution:
    def monkeyMove(self, n: int) -> int:
        mod = 10**9 + 7
        return (pow(2, n, mod) - 2) % mod

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
    public int monkeyMove(int n) {
        final int mod = (int) 1e9 + 7;
        return (qpow(2, n, mod) - 2 + mod) % mod;
    }

    private int qpow(long a, int n, int mod) {
        long ans = 1;
        for (; n > 0; n >>= 1) {
            if ((n & 1) == 1) {
                ans = ans * a % mod;
            }
            a = a * a % mod;
        }
        return (int) ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int monkeyMove(int n) {
        const int mod = 1e9 + 7;
        using ll = long long;
        auto qpow = [&](ll a, int n) {
            ll ans = 1;
            for (; n; n >>= 1) {
                if (n & 1) {
                    ans = ans * a % mod;
                }
                a = a * a % mod;
            }
            return ans;
        };
        return (qpow(2, n) - 2 + mod) % mod;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
func monkeyMove(n int) int {
    const mod = 1e9 + 7
    qpow := func(a, n int) int {
        ans := 1
        for ; n > 0; n >>= 1 {
            if n&1 == 1 {
                ans = ans * a % mod
            }
            a = a * a % mod
        }
        return ans
    }
    return (qpow(2, n) - 2 + mod) % mod
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
function monkeyMove(n: number): number {
    const mod = 10 ** 9 + 7;
    const qpow = (a: number, n: number): number => {
        let ans = 1n;
        for (; n; n >>>= 1) {
            if (n & 1) {
                ans = (ans * BigInt(a)) % BigInt(mod);
            }
            a = Number((BigInt(a) * BigInt(a)) % BigInt(mod));
        }
        return Number(ans);
    };
    return (qpow(2, n) - 2 + mod) % mod;
}

评论