2545. 根据第 K 场考试的分数排序

题目描述

班里有 m 位学生，共计划组织 n 场考试。给你一个下标从 0 开始、大小为 m x n 的整数矩阵 score ，其中每一行对应一位学生，而 score[i][j] 表示第 i 位学生在第 j 场考试取得的分数。矩阵 score 包含的整数 互不相同 。

另给你一个整数 k 。请你按第 k 场考试分数从高到低完成对这些学生（矩阵中的行）的排序。

返回排序后的矩阵。

示例 1：

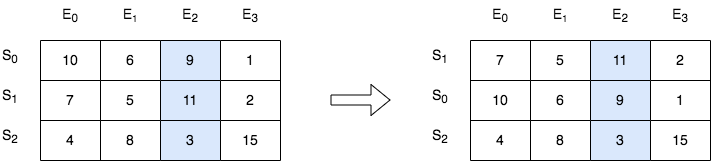
输入：score = [[10,6,9,1],[7,5,11,2],[4,8,3,15]], k = 2
输出：[[7,5,11,2],[10,6,9,1],[4,8,3,15]]
解释：在上图中，S 表示学生，E 表示考试。
- 下标为 1 的学生在第 2 场考试取得的分数为 11 ，这是考试的最高分，所以 TA 需要排在第一。
- 下标为 0 的学生在第 2 场考试取得的分数为 9 ，这是考试的第二高分，所以 TA 需要排在第二。
- 下标为 2 的学生在第 2 场考试取得的分数为 3 ，这是考试的最低分，所以 TA 需要排在第三。

示例 2：

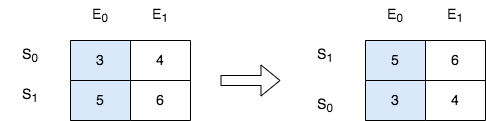
输入：score = [[3,4],[5,6]], k = 0
输出：[[5,6],[3,4]]
解释：在上图中，S 表示学生，E 表示考试。
- 下标为 1 的学生在第 0 场考试取得的分数为 5 ，这是考试的最高分，所以 TA 需要排在第一。
- 下标为 0 的学生在第 0 场考试取得的分数为 3 ，这是考试的最低分，所以 TA 需要排在第二。

提示：

m == score.length
n == score[i].length
1 <= m, n <= 250
1 <= score[i][j] <= 10⁵
score 由不同的整数组成
0 <= k < n

解法

方法一：排序

我们直接将 $\textit{score}$ 按照第 $k$ 列的分数从大到小排序，然后返回即可。

时间复杂度 $O(m \times \log m)$，空间复杂度 $O(\log m)$。其中 $m$ 为 $\textit{score}$ 的行数。

Python3JavaC++GoTypeScriptRust

class Solution:
    def sortTheStudents(self, score: List[List[int]], k: int) -> List[List[int]]:
        return sorted(score, key=lambda x: -x[k])

class Solution {
    public int[][] sortTheStudents(int[][] score, int k) {
        Arrays.sort(score, (a, b) -> b[k] - a[k]);
        return score;
    }
}

class Solution {
public:
    vector<vector<int>> sortTheStudents(vector<vector<int>>& score, int k) {
        ranges::sort(score, [k](const auto& a, const auto& b) { return a[k] > b[k]; });
        return score;
    }
};

func sortTheStudents(score [][]int, k int) [][]int {
    sort.Slice(score, func(i, j int) bool { return score[i][k] > score[j][k] })
    return score
}

function sortTheStudents(score: number[][], k: number): number[][] {
    return score.sort((a, b) => b[k] - a[k]);
}

impl Solution {
    pub fn sort_the_students(mut score: Vec<Vec<i32>>, k: i32) -> Vec<Vec<i32>> {
        let k = k as usize;
        score.sort_by(|a, b| b[k].cmp(&a[k]));
        score
    }
}

2545. 根据第 K 场考试的分数排序

题目描述

解法

方法一：排序

评论