2509. 查询树中环的长度

题目描述

给你一个整数 n ，表示你有一棵含有 2ⁿ - 1 个节点的 完全二叉树 。根节点的编号是 1 ，树中编号在[1, 2^{n - 1} - 1] 之间，编号为 val 的节点都有两个子节点，满足：

左子节点的编号为 2 * val
右子节点的编号为 2 * val + 1

给你一个长度为 m 的查询数组 queries ，它是一个二维整数数组，其中 queries[i] = [a_i, b_i] 。对于每个查询，求出以下问题的解：

在节点编号为 a_i 和 b_i 之间添加一条边。
求出图中环的长度。
删除节点编号为 a_i 和 b_i 之间新添加的边。

注意：

环是开始和结束于同一节点的一条路径，路径中每条边都只会被访问一次。
环的长度是环中边的数目。
在树中添加额外的边后，两个点之间可能会有多条边。

请你返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 个查询的结果。

示例 1：

输入：n = 3, queries = [[5,3],[4,7],[2,3]]
输出：[4,5,3]
解释：上图是一棵有 2³ - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 3 和节点 5 之间添加边后，环为 [5,2,1,3] ，所以第一个查询的结果是 4 。删掉添加的边后处理下一个查询。
- 在节点 4 和节点 7 之间添加边后，环为 [4,2,1,3,7] ，所以第二个查询的结果是 5 。删掉添加的边后处理下一个查询。
- 在节点 2 和节点 3 之间添加边后，环为 [2,1,3] ，所以第三个查询的结果是 3 。删掉添加的边。

示例 2：

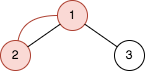
输入：n = 2, queries = [[1,2]]
输出：[2]
解释：上图是一棵有 2² - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 1 和节点 2 之间添加边后，环为 [2,1] ，所以第一个查询的结果是 2 。删掉添加的边。

提示：

2 <= n <= 30
m == queries.length
1 <= m <= 10⁵
queries[i].length == 2
1 <= a_i, b_i <= 2ⁿ - 1
a_i != b_i

解法

方法一：求最近公共祖先

对于每次查询，我们找出 $a$, $b$ 两个节点的最近公共祖先，并且记录向上走的步数，那么此次查询的答案就是步数加一。

求最近公共祖先时，如果 $a \gt b$，那么我们将 $a$ 往父节点移动；如果 $a \lt b$，我们将 $b$ 往其父节点移动。过程中累计步数，直至 $a = b$。

时间复杂度 $O(n \times m)$。其中 $m$ 为数组 queries 的长度。

Python3JavaC++Go

class Solution:
    def cycleLengthQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        ans = []
        for a, b in queries:
            t = 1
            while a != b:
                if a > b:
                    a >>= 1
                else:
                    b >>= 1
                t += 1
            ans.append(t)
        return ans

class Solution {
    public int[] cycleLengthQueries(int n, int[][] queries) {
        int m = queries.length;
        int[] ans = new int[m];
        for (int i = 0; i < m; ++i) {
            int a = queries[i][0], b = queries[i][1];
            int t = 1;
            while (a != b) {
                if (a > b) {
                    a >>= 1;
                } else {
                    b >>= 1;
                }
                ++t;
            }
            ans[i] = t;
        }
        return ans;
    }
}

class Solution {
public:
    vector<int> cycleLengthQueries(int n, vector<vector<int>>& queries) {
        vector<int> ans;
        for (auto& q : queries) {
            int a = q[0], b = q[1];
            int t = 1;
            while (a != b) {
                if (a > b) {
                    a >>= 1;
                } else {
                    b >>= 1;
                }
                ++t;
            }
            ans.emplace_back(t);
        }
        return ans;
    }
};

func cycleLengthQueries(n int, queries [][]int) []int {
    ans := []int{}
    for _, q := range queries {
        a, b := q[0], q[1]
        t := 1
        for a != b {
            if a > b {
                a >>= 1
            } else {
                b >>= 1
            }
            t++
        }
        ans = append(ans, t)
    }
    return ans
}

2509. 查询树中环的长度

题目描述

解法

方法一：求最近公共祖先

评论