


题目描述
给你一个正整数 n ,表示总共有 n 个城市,城市从 1 到 n 编号。给你一个二维数组 roads ,其中 roads[i] = [ai, bi, distancei] 表示城市 ai 和 bi 之间有一条 双向 道路,道路距离为 distancei 。城市构成的图不一定是连通的。
两个城市之间一条路径的 分数 定义为这条路径中道路的 最小 距离。
城市 1 和城市 n 之间的所有路径的 最小 分数。
注意:
- 一条路径指的是两个城市之间的道路序列。
- 一条路径可以 多次 包含同一条道路,你也可以沿着路径多次到达城市
1 和城市 n 。
- 测试数据保证城市
1 和城市n 之间 至少 有一条路径。
示例 1:
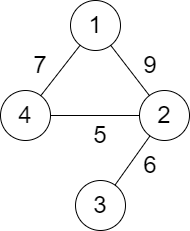
输入:n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
输出:5
解释:城市 1 到城市 4 的路径中,分数最小的一条为:1 -> 2 -> 4 。这条路径的分数是 min(9,5) = 5 。
不存在分数更小的路径。
示例 2:
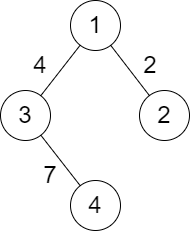
输入:n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
输出:2
解释:城市 1 到城市 4 分数最小的路径是:1 -> 2 -> 1 -> 3 -> 4 。这条路径的分数是 min(2,2,4,7) = 2 。
提示:
2 <= n <= 1051 <= roads.length <= 105roads[i].length == 31 <= ai, bi <= nai != bi1 <= distancei <= 104- 不会有重复的边。
- 城市
1 和城市 n 之间至少有一条路径。
解法
方法一:DFS
根据题目描述,每条边可以经过多次,并且保证节点 \(1\) 和节点 \(n\) 在同一个连通块中。因此,题目实际上求的是节点 \(1\) 所在的连通块的最小边。我们可以用 DFS,从节点 \(1\) 开始搜索所有的边,找到最小的边即可。
时间复杂度 \(O(n + m)\)。其中 \(n\) 和 \(m\) 分别是节点数和边数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | class Solution:
def minScore(self, n: int, roads: List[List[int]]) -> int:
def dfs(i):
nonlocal ans
for j, d in g[i]:
ans = min(ans, d)
if not vis[j]:
vis[j] = True
dfs(j)
g = defaultdict(list)
for a, b, d in roads:
g[a].append((b, d))
g[b].append((a, d))
vis = [False] * (n + 1)
ans = inf
dfs(1)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | class Solution {
private List<int[]>[] g;
private boolean[] vis;
private int ans = 1 << 30;
public int minScore(int n, int[][] roads) {
g = new List[n];
vis = new boolean[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : roads) {
int a = e[0] - 1, b = e[1] - 1, d = e[2];
g[a].add(new int[] {b, d});
g[b].add(new int[] {a, d});
}
dfs(0);
return ans;
}
private void dfs(int i) {
for (var nxt : g[i]) {
int j = nxt[0], d = nxt[1];
ans = Math.min(ans, d);
if (!vis[j]) {
vis[j] = true;
dfs(j);
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | class Solution {
public:
int minScore(int n, vector<vector<int>>& roads) {
vector<vector<pair<int, int>>> g(n);
bool vis[n];
memset(vis, 0, sizeof vis);
for (auto& e : roads) {
int a = e[0] - 1, b = e[1] - 1, d = e[2];
g[a].emplace_back(b, d);
g[b].emplace_back(a, d);
}
int ans = INT_MAX;
function<void(int)> dfs = [&](int i) {
for (auto [j, d] : g[i]) {
ans = min(ans, d);
if (!vis[j]) {
vis[j] = true;
dfs(j);
}
}
};
dfs(0);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | func minScore(n int, roads [][]int) int {
type pair struct{ i, v int }
g := make([][]pair, n)
for _, e := range roads {
a, b, d := e[0]-1, e[1]-1, e[2]
g[a] = append(g[a], pair{b, d})
g[b] = append(g[b], pair{a, d})
}
vis := make([]bool, n)
ans := 1 << 30
var dfs func(int)
dfs = func(i int) {
for _, nxt := range g[i] {
j, d := nxt.i, nxt.v
ans = min(ans, d)
if !vis[j] {
vis[j] = true
dfs(j)
}
}
}
dfs(0)
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | function minScore(n: number, roads: number[][]): number {
const vis = new Array(n + 1).fill(false);
const g = Array.from({ length: n + 1 }, () => []);
for (const [a, b, v] of roads) {
g[a].push([b, v]);
g[b].push([a, v]);
}
let ans = Infinity;
const dfs = (i: number) => {
if (vis[i]) {
return;
}
vis[i] = true;
for (const [j, v] of g[i]) {
ans = Math.min(ans, v);
dfs(j);
}
};
dfs(1);
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | impl Solution {
fn dfs(i: usize, mut ans: i32, g: &Vec<Vec<(usize, i32)>>, vis: &mut Vec<bool>) -> i32 {
if vis[i] {
return ans;
}
vis[i] = true;
for (j, v) in g[i].iter() {
ans = ans.min(*v.min(&Self::dfs(*j, ans, g, vis)));
}
ans
}
pub fn min_score(n: i32, roads: Vec<Vec<i32>>) -> i32 {
let n = n as usize;
let mut vis = vec![false; n + 1];
let mut g = vec![Vec::new(); n + 1];
for road in roads.iter() {
let a = road[0] as usize;
let b = road[1] as usize;
let v = road[2];
g[a].push((b, v));
g[b].push((a, v));
}
Self::dfs(1, i32::MAX, &g, &mut vis)
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | var minScore = function (n, roads) {
// 构建点到点的映射表
const graph = Array.from({ length: n + 1 }, () => new Map());
for (let [u, v, w] of roads) {
graph[u].set(v, w);
graph[v].set(u, w);
}
// DFS
const vis = new Array(n).fill(false);
let ans = Infinity;
var dfs = function (u) {
vis[u] = true;
for (const [v, w] of graph[u]) {
ans = Math.min(ans, w);
if (!vis[v]) dfs(v);
}
};
dfs(1);
return ans;
};
|
方法二:BFS
我们也可以用 BFS 来求解。
时间复杂度 \(O(n + m)\)。其中 \(n\) 和 \(m\) 分别是节点数和边数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | class Solution:
def minScore(self, n: int, roads: List[List[int]]) -> int:
g = defaultdict(list)
for a, b, d in roads:
g[a].append((b, d))
g[b].append((a, d))
vis = [False] * (n + 1)
vis[1] = True
ans = inf
q = deque([1])
while q:
for _ in range(len(q)):
i = q.popleft()
for j, d in g[i]:
ans = min(ans, d)
if not vis[j]:
vis[j] = True
q.append(j)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | class Solution {
public int minScore(int n, int[][] roads) {
List<int[]>[] g = new List[n];
boolean[] vis = new boolean[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : roads) {
int a = e[0] - 1, b = e[1] - 1, d = e[2];
g[a].add(new int[] {b, d});
g[b].add(new int[] {a, d});
}
Deque<Integer> q = new ArrayDeque<>();
q.offer(0);
vis[0] = true;
int ans = 1 << 30;
while (!q.isEmpty()) {
for (int k = q.size(); k > 0; --k) {
int i = q.pollFirst();
for (var nxt : g[i]) {
int j = nxt[0], d = nxt[1];
ans = Math.min(ans, d);
if (!vis[j]) {
vis[j] = true;
q.offer(j);
}
}
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | class Solution {
public:
int minScore(int n, vector<vector<int>>& roads) {
vector<vector<pair<int, int>>> g(n);
bool vis[n];
memset(vis, 0, sizeof vis);
for (auto& e : roads) {
int a = e[0] - 1, b = e[1] - 1, d = e[2];
g[a].emplace_back(b, d);
g[b].emplace_back(a, d);
}
int ans = INT_MAX;
queue<int> q{{0}};
vis[0] = true;
while (!q.empty()) {
for (int k = q.size(); k; --k) {
int i = q.front();
q.pop();
for (auto [j, d] : g[i]) {
ans = min(ans, d);
if (!vis[j]) {
vis[j] = true;
q.push(j);
}
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | func minScore(n int, roads [][]int) int {
type pair struct{ i, v int }
g := make([][]pair, n)
for _, e := range roads {
a, b, d := e[0]-1, e[1]-1, e[2]
g[a] = append(g[a], pair{b, d})
g[b] = append(g[b], pair{a, d})
}
vis := make([]bool, n)
ans := 1 << 30
q := []int{0}
vis[0] = true
for len(q) > 0 {
for k := len(q); k > 0; k-- {
i := q[0]
q = q[1:]
for _, nxt := range g[i] {
j, d := nxt.i, nxt.v
ans = min(ans, d)
if !vis[j] {
vis[j] = true
q = append(q, j)
}
}
}
}
return ans
}
|




