
题目描述
有一个无向树,有 n 个节点,节点标记为从 0 到 n - 1。给定整数 n 和一个长度为 n - 1 的 2 维整数数组 edges,其中 edges[i] = [ai, bi] 表示在树中的节点 ai 和 bi 之间有一条边。树的根节点是标记为 0 的节点。
每个节点都有一个相关联的 值。给定一个长度为 n 的数组 values,其中 values[i] 是第 i 个节点的 值。
选择任意两个 不重叠 的子树。你的 分数 是这些子树中值的和的逐位异或。
返回你能达到的最大分数。如果不可能找到两个不重叠的子树,则返回 0。
注意:
- 节点的 子树 是由该节点及其所有子节点组成的树。
- 如果两个子树不共享 任何公共 节点,则它们是 不重叠 的。
示例 1:
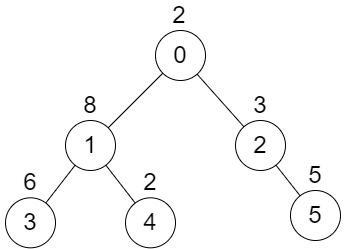
输入: n = 6, edges = [[0,1],[0,2],[1,3],[1,4],[2,5]], values = [2,8,3,6,2,5]
输出: 24
解释: 节点 1 的子树的和值为 16,而节点 2 的子树的和值为 8,因此选择这些节点将得到 16 XOR 8 = 24 的分数。可以证明,这是我们能得到的最大可能分数。
示例 2:
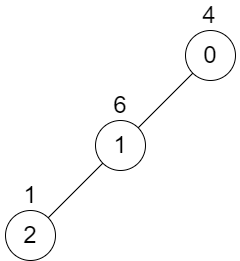
输入: n = 3, edges = [[0,1],[1,2]], values = [4,6,1]
输出: 0
解释: 不可能选择两个不重叠的子树,所以我们只返回 0。
提示:
2 <= n <= 5 * 104edges.length == n - 10 <= ai, bi < nvalues.length == n1 <= values[i] <= 109- 保证
edges 代表一个有效的树。
解法
方法一:递归 + 0-1 前缀树
我们先递归预处理出每个节点的子树和,记录在数组 \(s\) 中。
然后使用 0-1 前缀树维护遍历过的子树和,可以方便快速查找下一个子树和与之前的子树和的最大异或值。
由于子树不能重叠,因此,我们先查询最大异或值,递归结束后,再将当前子树和插入到前缀树中。
时间复杂度 \(O(n \times log M)\),其中 \(n\) 为节点个数,而 \(M\) 为子树和的最大值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 | class Trie:
def __init__(self):
self.children = [None] * 2
def insert(self, x):
node = self
for i in range(47, -1, -1):
v = (x >> i) & 1
if node.children[v] is None:
node.children[v] = Trie()
node = node.children[v]
def search(self, x):
node = self
res = 0
for i in range(47, -1, -1):
v = (x >> i) & 1
if node is None:
return res
if node.children[v ^ 1]:
res = res << 1 | 1
node = node.children[v ^ 1]
else:
res <<= 1
node = node.children[v]
return res
class Solution:
def maxXor(self, n: int, edges: List[List[int]], values: List[int]) -> int:
def dfs1(i, fa):
t = values[i]
for j in g[i]:
if j != fa:
t += dfs1(j, i)
s[i] = t
return t
def dfs2(i, fa):
nonlocal ans
ans = max(ans, tree.search(s[i]))
for j in g[i]:
if j != fa:
dfs2(j, i)
tree.insert(s[i])
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
s = [0] * n
dfs1(0, -1)
ans = 0
tree = Trie()
dfs2(0, -1)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78 | class Trie {
Trie[] children = new Trie[2];
void insert(long x) {
Trie node = this;
for (int i = 47; i >= 0; --i) {
int v = (int) (x >> i) & 1;
if (node.children[v] == null) {
node.children[v] = new Trie();
}
node = node.children[v];
}
}
long search(long x) {
Trie node = this;
long res = 0;
for (int i = 47; i >= 0; --i) {
int v = (int) (x >> i) & 1;
if (node == null) {
return res;
}
if (node.children[v ^ 1] != null) {
res = res << 1 | 1;
node = node.children[v ^ 1];
} else {
res <<= 1;
node = node.children[v];
}
}
return res;
}
}
class Solution {
private List<Integer>[] g;
private int[] vals;
private long[] s;
private Trie tree;
private long ans;
public long maxXor(int n, int[][] edges, int[] values) {
g = new List[n];
s = new long[n];
vals = values;
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
dfs1(0, -1);
tree = new Trie();
dfs2(0, -1);
return ans;
}
private void dfs2(int i, int fa) {
ans = Math.max(ans, tree.search(s[i]));
for (int j : g[i]) {
if (j != fa) {
dfs2(j, i);
}
}
tree.insert(s[i]);
}
private long dfs1(int i, int fa) {
long t = vals[i];
for (int j : g[i]) {
if (j != fa) {
t += dfs1(j, i);
}
}
s[i] = t;
return t;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70 | using ll = long long;
class Trie {
public:
vector<Trie*> children;
string v;
Trie()
: children(2) {}
void insert(ll x) {
Trie* node = this;
for (int i = 47; ~i; --i) {
int v = (x >> i) & 1;
if (!node->children[v]) node->children[v] = new Trie();
node = node->children[v];
}
}
ll search(ll x) {
Trie* node = this;
ll res = 0;
for (int i = 47; ~i; --i) {
if (!node) return res;
int v = (x >> i) & 1;
if (node->children[v ^ 1]) {
res = res << 1 | 1;
node = node->children[v ^ 1];
} else {
res <<= 1;
node = node->children[v];
}
}
return res;
}
};
class Solution {
public:
long long maxXor(int n, vector<vector<int>>& edges, vector<int>& values) {
vector<vector<int>> g(n);
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].emplace_back(b);
g[b].emplace_back(a);
}
vector<ll> s(n);
function<ll(int, int)> dfs1 = [&](int i, int fa) -> ll {
ll t = values[i];
for (int j : g[i]) {
if (j != fa) t += dfs1(j, i);
}
s[i] = t;
return t;
};
dfs1(0, -1);
Trie tree;
ll ans = 0;
function<void(int, int)> dfs2 = [&](int i, int fa) {
ans = max(ans, tree.search(s[i]));
for (int j : g[i]) {
if (j != fa) {
dfs2(j, i);
}
}
tree.insert(s[i]);
};
dfs2(0, -1);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73 | type Trie struct {
children [2]*Trie
}
func newTrie() *Trie {
return &Trie{}
}
func (this *Trie) insert(x int) {
node := this
for i := 47; i >= 0; i-- {
v := (x >> i) & 1
if node.children[v] == nil {
node.children[v] = newTrie()
}
node = node.children[v]
}
}
func (this *Trie) search(x int) int {
node := this
res := 0
for i := 47; i >= 0; i-- {
v := (x >> i) & 1
if node == nil {
return res
}
if node.children[v^1] != nil {
res = res<<1 | 1
node = node.children[v^1]
} else {
res <<= 1
node = node.children[v]
}
}
return res
}
func maxXor(n int, edges [][]int, values []int) int64 {
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
s := make([]int, n)
var dfs1 func(i, fa int) int
dfs1 = func(i, fa int) int {
t := values[i]
for _, j := range g[i] {
if j != fa {
t += dfs1(j, i)
}
}
s[i] = t
return t
}
dfs1(0, -1)
ans := 0
tree := newTrie()
var dfs2 func(i, fa int)
dfs2 = func(i, fa int) {
ans = max(ans, tree.search(s[i]))
for _, j := range g[i] {
if j != fa {
dfs2(j, i)
}
}
tree.insert(s[i])
}
dfs2(0, -1)
return int64(ans)
}
|


