


题目描述
给你一棵 n 个节点的树(连通无向无环的图),节点编号从 0 到 n - 1 且恰好有 n - 1 条边。
给你一个长度为 n 下标从 0 开始的整数数组 vals ,分别表示每个节点的值。同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
一条 好路径 需要满足以下条件:
- 开始节点和结束节点的值 相同 。
- 开始节点和结束节点中间的所有节点值都 小于等于 开始节点的值(也就是说开始节点的值应该是路径上所有节点的最大值)。
请你返回不同好路径的数目。
注意,一条路径和它反向的路径算作 同一 路径。比方说, 0 -> 1 与 1 -> 0 视为同一条路径。单个节点也视为一条合法路径。
示例 1:
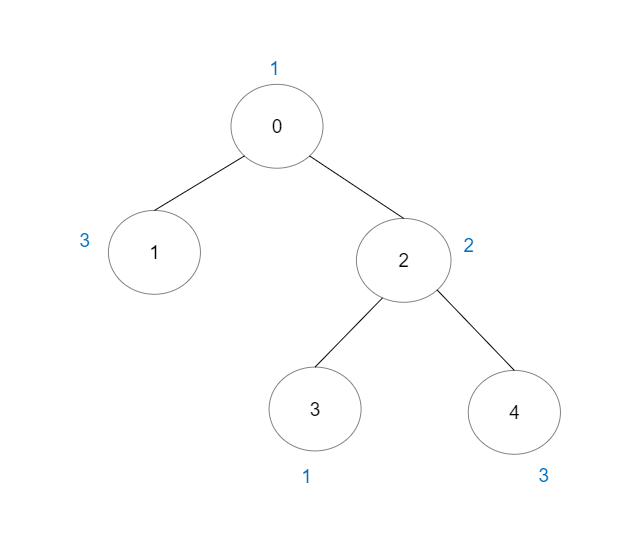
输入:vals = [1,3,2,1,3], edges = [[0,1],[0,2],[2,3],[2,4]]
输出:6
解释:总共有 5 条单个节点的好路径。
还有 1 条好路径:1 -> 0 -> 2 -> 4 。
(反方向的路径 4 -> 2 -> 0 -> 1 视为跟 1 -> 0 -> 2 -> 4 一样的路径)
注意 0 -> 2 -> 3 不是一条好路径,因为 vals[2] > vals[0] 。
示例 2:
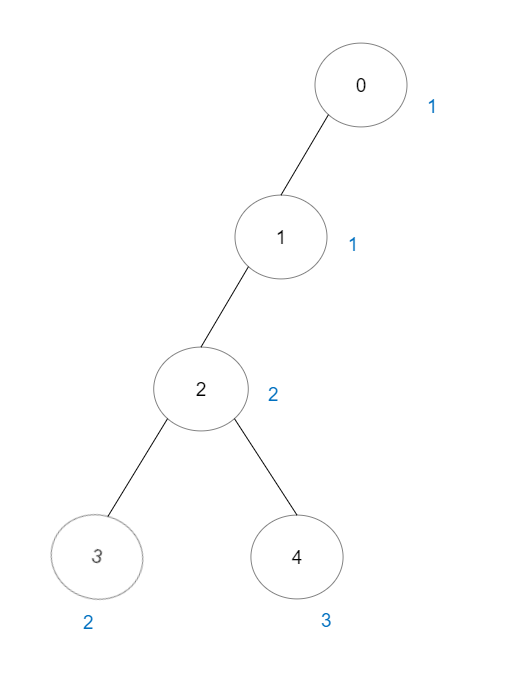
输入:vals = [1,1,2,2,3], edges = [[0,1],[1,2],[2,3],[2,4]]
输出:7
解释:总共有 5 条单个节点的好路径。
还有 2 条好路径:0 -> 1 和 2 -> 3 。
示例 3:
输入:vals = [1], edges = []
输出:1
解释:这棵树只有一个节点,所以只有一条好路径。
提示:
n == vals.length1 <= n <= 3 * 1040 <= vals[i] <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges 表示一棵合法的树。
解法
方法一:排序 + 并查集
要保证路径起点(终点)大于等于路径上的所有点,因此我们可以考虑先把所有点按值从小到大排序,然后再进行遍历,添加到连通块中,具体如下:
当遍历到点 \(a\) 时, 对于小于等于 \(vals[a]\) 的邻接点 \(b\) 来说,若二者不在同一个连通块,则可以合并,并且可以以点 \(a\) 所在的连通块中所有值为 \(vals[a]\) 的点为起点,以点 \(b\) 所在的连通块中所有值为 \(vals[a]\) 的点为终点,两种点的个数的乘积即为加入点 \(a\) 时对答案的贡献。
时间复杂度 \(O(n \times \log n)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | class Solution:
def numberOfGoodPaths(self, vals: List[int], edges: List[List[int]]) -> int:
def find(x):
if p[x] != x:
p[x] = find(p[x])
return p[x]
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
n = len(vals)
p = list(range(n))
size = defaultdict(Counter)
for i, v in enumerate(vals):
size[i][v] = 1
ans = n
for v, a in sorted(zip(vals, range(n))):
for b in g[a]:
if vals[b] > v:
continue
pa, pb = find(a), find(b)
if pa != pb:
ans += size[pa][v] * size[pb][v]
p[pa] = pb
size[pb][v] += size[pa][v]
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 | class Solution {
private int[] p;
public int numberOfGoodPaths(int[] vals, int[][] edges) {
int n = vals.length;
p = new int[n];
int[][] arr = new int[n][2];
List<Integer>[] g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (int[] e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
Map<Integer, Map<Integer, Integer>> size = new HashMap<>();
for (int i = 0; i < n; ++i) {
p[i] = i;
arr[i] = new int[] {vals[i], i};
size.computeIfAbsent(i, k -> new HashMap<>()).put(vals[i], 1);
}
Arrays.sort(arr, (a, b) -> a[0] - b[0]);
int ans = n;
for (var e : arr) {
int v = e[0], a = e[1];
for (int b : g[a]) {
if (vals[b] > v) {
continue;
}
int pa = find(a), pb = find(b);
if (pa != pb) {
ans += size.get(pa).getOrDefault(v, 0) * size.get(pb).getOrDefault(v, 0);
p[pa] = pb;
size.get(pb).put(
v, size.get(pb).getOrDefault(v, 0) + size.get(pa).getOrDefault(v, 0));
}
}
}
return ans;
}
private int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 | class Solution {
public:
int numberOfGoodPaths(vector<int>& vals, vector<vector<int>>& edges) {
int n = vals.size();
vector<int> p(n);
iota(p.begin(), p.end(), 0);
function<int(int)> find;
find = [&](int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
};
vector<vector<int>> g(n);
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
unordered_map<int, unordered_map<int, int>> size;
vector<pair<int, int>> arr(n);
for (int i = 0; i < n; ++i) {
arr[i] = {vals[i], i};
size[i][vals[i]] = 1;
}
sort(arr.begin(), arr.end());
int ans = n;
for (auto [v, a] : arr) {
for (int b : g[a]) {
if (vals[b] > v) {
continue;
}
int pa = find(a), pb = find(b);
if (pa != pb) {
ans += size[pa][v] * size[pb][v];
p[pa] = pb;
size[pb][v] += size[pa][v];
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 | func numberOfGoodPaths(vals []int, edges [][]int) int {
n := len(vals)
p := make([]int, n)
size := map[int]map[int]int{}
type pair struct{ v, i int }
arr := make([]pair, n)
for i, v := range vals {
p[i] = i
if size[i] == nil {
size[i] = map[int]int{}
}
size[i][v] = 1
arr[i] = pair{v, i}
}
var find func(x int) int
find = func(x int) int {
if p[x] != x {
p[x] = find(p[x])
}
return p[x]
}
sort.Slice(arr, func(i, j int) bool { return arr[i].v < arr[j].v })
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
ans := n
for _, e := range arr {
v, a := e.v, e.i
for _, b := range g[a] {
if vals[b] > v {
continue
}
pa, pb := find(a), find(b)
if pa != pb {
ans += size[pb][v] * size[pa][v]
p[pa] = pb
size[pb][v] += size[pa][v]
}
}
}
return ans
}
|





