二叉树
哈希表
广度优先搜索
树
深度优先搜索
题目描述
给你一棵二叉树的根节点 root ,二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟,感染 将会从值为 start 的节点开始爆发。
每分钟,如果节点满足以下全部条件,就会被感染:
返回感染整棵树需要的分钟数。
示例 1:
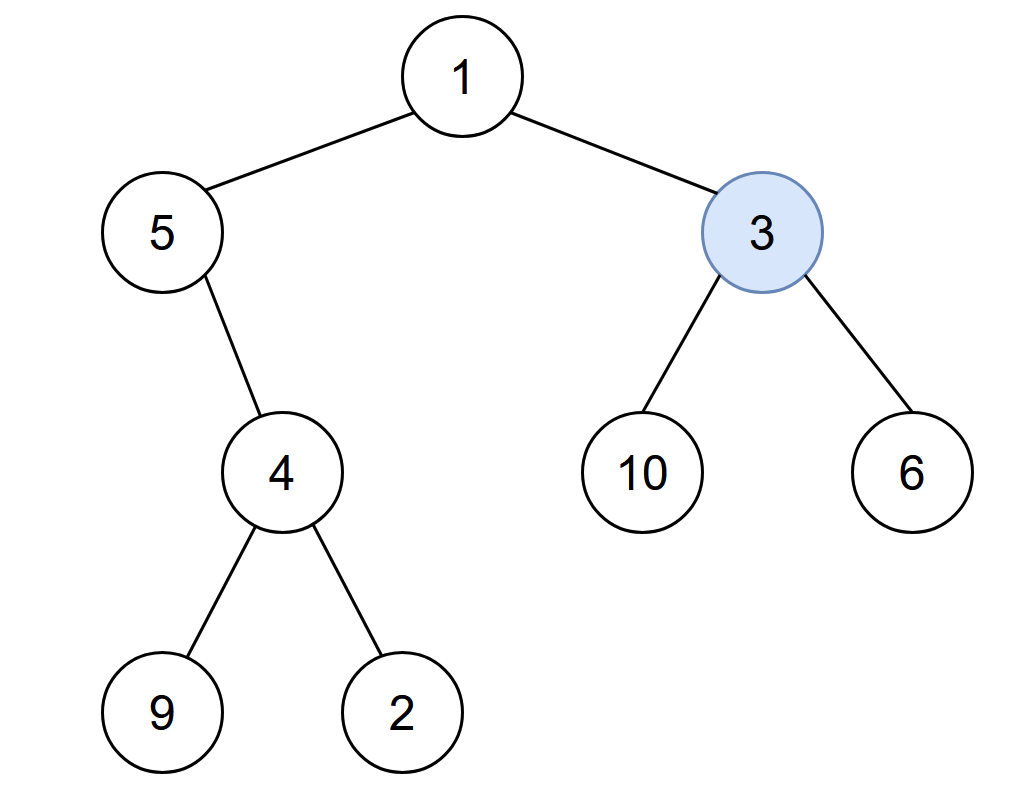
输入: root = [1,5,3,null,4,10,6,9,2], start = 3
输出: 4
解释: 节点按以下过程被感染:
- 第 0 分钟:节点 3
- 第 1 分钟:节点 1、10、6
- 第 2 分钟:节点5
- 第 3 分钟:节点 4
- 第 4 分钟:节点 9 和 2
感染整棵树需要 4 分钟,所以返回 4 。
示例 2:
输入: root = [1], start = 1
输出: 0
解释: 第 0 分钟,树中唯一一个节点处于感染状态,返回 0 。
提示:
树中节点的数目在范围 [1, 105 ] 内
1 <= Node.val <= 105 每个节点的值 互不相同
树中必定存在值为 start 的节点
解法
方法一:两次 DFS
我们先通过一次 \(\textit{DFS}\) 建图,得到一个邻接表 \(g\) ,其中 \(g[node]\) 表示与节点 \(node\) 相连的所有节点。
然后,我们以 \(start\) 作为起点,通过 \(\textit{DFS}\) 搜索整棵树,找到最远距离,即为答案。
时间复杂度 \(O(n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 为二叉树的节点个数。
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def amountOfTime ( self , root : Optional [ TreeNode ], start : int ) -> int :
def dfs ( node : Optional [ TreeNode ], fa : Optional [ TreeNode ]):
if node is None :
return
if fa :
g [ node . val ] . append ( fa . val )
g [ fa . val ] . append ( node . val )
dfs ( node . left , node )
dfs ( node . right , node )
def dfs2 ( node : int , fa : int ) -> int :
ans = 0
for nxt in g [ node ]:
if nxt != fa :
ans = max ( ans , 1 + dfs2 ( nxt , node ))
return ans
g = defaultdict ( list )
dfs ( root , None )
return dfs2 ( start , - 1 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private Map < Integer , List < Integer >> g = new HashMap <> ();
public int amountOfTime ( TreeNode root , int start ) {
dfs ( root , null );
return dfs2 ( start , - 1 );
}
private void dfs ( TreeNode node , TreeNode fa ) {
if ( node == null ) {
return ;
}
if ( fa != null ) {
g . computeIfAbsent ( node . val , k -> new ArrayList <> ()). add ( fa . val );
g . computeIfAbsent ( fa . val , k -> new ArrayList <> ()). add ( node . val );
}
dfs ( node . left , node );
dfs ( node . right , node );
}
private int dfs2 ( int node , int fa ) {
int ans = 0 ;
for ( int nxt : g . getOrDefault ( node , List . of ())) {
if ( nxt != fa ) {
ans = Math . max ( ans , 1 + dfs2 ( nxt , node ));
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
int amountOfTime ( TreeNode * root , int start ) {
unordered_map < int , vector < int >> g ;
function < void ( TreeNode * , TreeNode * ) > dfs = [ & ]( TreeNode * node , TreeNode * fa ) {
if ( ! node ) {
return ;
}
if ( fa ) {
g [ node -> val ]. push_back ( fa -> val );
g [ fa -> val ]. push_back ( node -> val );
}
dfs ( node -> left , node );
dfs ( node -> right , node );
};
function < int ( int , int ) > dfs2 = [ & ]( int node , int fa ) -> int {
int ans = 0 ;
for ( int nxt : g [ node ]) {
if ( nxt != fa ) {
ans = max ( ans , 1 + dfs2 ( nxt , node ));
}
}
return ans ;
};
dfs ( root , nullptr );
return dfs2 ( start , -1 );
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func amountOfTime ( root * TreeNode , start int ) int {
g := map [ int ][] int {}
var dfs func ( * TreeNode , * TreeNode )
dfs = func ( node , fa * TreeNode ) {
if node == nil {
return
}
if fa != nil {
g [ node . Val ] = append ( g [ node . Val ], fa . Val )
g [ fa . Val ] = append ( g [ fa . Val ], node . Val )
}
dfs ( node . Left , node )
dfs ( node . Right , node )
}
var dfs2 func ( int , int ) int
dfs2 = func ( node , fa int ) ( ans int ) {
for _ , nxt := range g [ node ] {
if nxt != fa {
ans = max ( ans , 1 + dfs2 ( nxt , node ))
}
}
return
}
dfs ( root , nil )
return dfs2 ( start , - 1 )
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function amountOfTime ( root : TreeNode | null , start : number ) : number {
const g : Map < number , number [] > = new Map ();
const dfs = ( node : TreeNode | null , fa : TreeNode | null ) => {
if ( ! node ) {
return ;
}
if ( fa ) {
if ( ! g . has ( node . val )) {
g . set ( node . val , []);
}
g . get ( node . val ) ! . push ( fa . val );
if ( ! g . has ( fa . val )) {
g . set ( fa . val , []);
}
g . get ( fa . val ) ! . push ( node . val );
}
dfs ( node . left , node );
dfs ( node . right , node );
};
const dfs2 = ( node : number , fa : number ) : number => {
let ans = 0 ;
for ( const nxt of g . get ( node ) || []) {
if ( nxt !== fa ) {
ans = Math . max ( ans , 1 + dfs2 ( nxt , node ));
}
}
return ans ;
};
dfs ( root , null );
return dfs2 ( start , - 1 );
}
GitHub